现在我们再回顾一下整个第三章所学的内容，再把头绪整理一下，进一步明确这一章所要掌握的主要内容，如有些部分仍不清楚，则可以再返回去学习与思考一下。 　　一、参数判别分类方法与非参数判别分类方法的区别 　　经过这一章的学习，我们应该对非线性分类判别方法与参数分类判别方法之间的区别有更清楚的认识了。从参数判别方法看，它的前提是对特征空间中的各类样本的分布清楚，因此一旦要测试分类样本的特征向量值X已知，就可以确定X对各类的后验概率，也就可按相应的准则计算与分类。如果这种分布可以用正态分布等描述，那么决策域的判别函数与分界面方程就可用函数的形式确定下来。所以判别函数等的确定取决于样本统计分布的有关知识。因此参数分类判别方法一般只能用在有统计知识的场合，或能利用训练样本估计出参数的场合。 而非参数分类判别方法则着眼于直接利用训练样本集，省去参数估计这一环节，这样一来，从保证最小错误率的原则出发计算确定判别函数的方法就不适用了。因此非参数分类判别方法只能根据一些其它准则来设计分类器。分类器的效果好坏，常指分类的错误率，一般在理论上很难说明，主要靠实践来检验。所选择的判别函数型式，所使用的训练样本集，以及所用的算法对结果都会有影响。 　　二、非参数分类判别方法的基本做法 　　使用非参数分类判别方法进行分类器设计主要包含两个步骤：一个是确定的使用的判别函数类型或决策面方程类型，如线性分类器，分段线性分类器，非线性分类器等或近邻法等。如果使用人工神经元网络，则怎样的网络结构也隐含了所使用的函数形式。另一个步骤是在选定的函数类型网络结构等条件下，确定相应的参数，从而完成整个分类器设计。 　　三、决策面方程的显式表示和隐式表示 　　对一个分类的决策域划分一般可采用两种形式，一种是用函数直接表示分界面方程，如线性方程式表示的边界等。另一种则用隐含形式，例如我们用最小距离分类器就代表了这种类型，其实这两种形式是等价的。如二维空间的最小距离分类器用最小距离表示为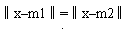：，而其等价于连接m1与m2线的垂直平分线 。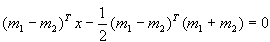本章学习的Fisher准则、支持向量机与局部训练法等用的是显式表示，而错误修正法和近邻法则可以说是隐式表示。 　　四、基于相似度的分类判别方法 　　判别函数的隐式表示与使用基于相似度判别的原则有关。如近邻法是用距离远近表示相似程度，错误修正法用样本向量与增广权向量的点积运算，也可在一定程度上看作相似度。在多类问题上，往往用计算相似度较方便。 　　五、Fisher准则 　　Fisher准则是传统模式识别方法中的典型方法，它强调将线性方程中的法向量与样本的乘积看作样本向量在单位法向量上的投影，如能做到不同类的样本在法向量上的投影呈现类内聚集，类向分开的效果，则对减少错分类有利。所得最佳法向量计算式为 (见有关课文定义)。这个结果与正态分布协方差矩阵等的贝叶斯决策结果相似，这说明如果两类分布围绕各自均值的确相近，Fisher准则可使错误率较小。 　　六、感知准则函数方法 　　这种方法提倡用错分类提供的信息修正错误，这种思想对机器学习的发展以及人工神经元网络的发生发展产生深远影响。 　　七、近邻法 　　近邻法训练样本数量较多时，从渐近错误率角度看，其错误率比较小，是经常使用的模式识别分类方法，比较适合在多类别情况下使用。当每类的样本数很多时，存储量与计算量要求都偏高，使用剪辑近邻法与压缩近邻法，特别是压缩近邻法可大量减少训练样本的数量。 　　八、支持向量机 　　支持向量机是新近提出的影响较大的方法。在理论上有很深的背景，这里指的理论是统计学习理论。它主要关注的问题是：当训练样本数量有限时。在训练过程中做到使训练样本错误率为最小，是否就意味着系统在实际运用中，也能自然而然做到错误率小呢？对我们来说了解这种理论显然超出我们课程的范围。但是可以举一个例子说明这种问题的确存在。例如下图表示在一个样本集(X,Y)，其中X在实数范围内取值，而Y则在[+1，-1]范围内取值。 　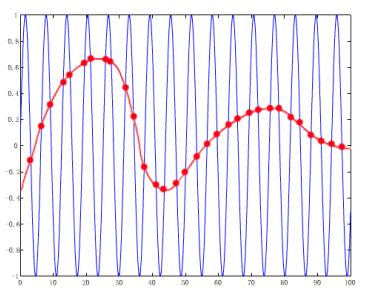　红线表示正确拟合得到的结果，但是对于这样一组数据，我们完全可以用一个函数Sin(ax)来拟合它，如图中蓝线表示的函数所示，只要调整参数a总可以使所有数据都落在Sin(ax)曲线上，但是很明显Sin(ax)并不反映这组数据的内在规律，如果再增加一个新数据，参数a很可能就要变。从直观上讲，所用的函数Sin(ax)并不合适，但是从训练样本数据来看，它的拟合程度的确很高。这种问题其实并不是偶然现象，从我们所讨论的一些方法中,分类器设计的性能，都以对训练样本集有好的性能为目标，而没有办法保证在实际使用时仍能保持好的性能。支持向量机在线性可分时要求隔离带尽可能宽，正是从期望实际的错误率也较低这一点出发的。关于这一点需要很深的理论，我们只做一种浅显的解释。对我们的实际应用来说，支持向量机可以通过特征映射方法,将原特征空间需要用非线性函数分类的问题，转换成在一个新的空间中仍然采用线性分类器的方法，使实际使用非线性分类器(而不是分段线性分类器)的可能性大大增加。这是一个很大的突破。