3.3.4.1 紧互对原型与交遇区
这一节提出寻找“交遇区”的一种方法,其实质是先在每类样本集内进行分片划分,所使用的方法是聚类方法,这在第五章会讨论。也可以采用别的方法。划分的目的是使每类样本划分成小片后,找到处在本类样本占领区域边界上的小片原型。找到边界子集的方法是通过与另一类样本子集中找近邻的方法实现的。如果发现分属两类的两个原型互为最近邻,那么这两个原型就被认定为处在两类样本决策域的交界处,它们所在区域就成为交遇区。交遇区就是有这些处在边界上的原型集组成。为了简便计算,每个小片(原型)都找出一质心,用它代表这个小片(也称原型)。通过计算每个原型与其它原型的欧氏距离来计算近邻关系。
为了找到两类样本的交遇区,首先对这两类样本进行聚类分析,从而找出它们各自的一些相对密集的子区域,称为“原型区”。图3.15中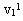 , ,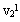 , ,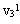 ,等是ω1的若干个原型区,而V21, ,等是ω1的若干个原型区,而V21, 与 与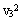 等是ω2的原型区。在每个原型区中找到一个质心或距质心很近的样本作为各原型区的代表点,称为“原型”。然后在两个类别的原型集合中,分别计算不同类原型对之间的欧氏距离,并找出各原型在对方类型中相距最近的原型对,如v21的最近原型是 等是ω2的原型区。在每个原型区中找到一个质心或距质心很近的样本作为各原型区的代表点,称为“原型”。然后在两个类别的原型集合中,分别计算不同类原型对之间的欧氏距离,并找出各原型在对方类型中相距最近的原型对,如v21的最近原型是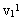 ,而 ,而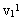 的最近原型是 的最近原型是 等。从这些最小距离原型关系中找到互为最小距离的原型对,如v12与v23,组成所谓“紧互对原型对”。紧互对原型对的集合组成“交遇区”。有时可将紧互对原型对扩展成k-紧互对原型对,即将找一个最近的原型改成找k个最近的原型。 等。从这些最小距离原型关系中找到互为最小距离的原型对,如v12与v23,组成所谓“紧互对原型对”。紧互对原型对的集合组成“交遇区”。有时可将紧互对原型对扩展成k-紧互对原型对,即将找一个最近的原型改成找k个最近的原型。
3.3.4.2 局部训练法
这一节讲如何利用“交遇区”来设计分界面的问题。基本思想是边界由若干个交遇区确定,在每个交遇区中只有两种不同类型的样本。由这些样本产生一个合适的分界面,一般使用分段线性分界面。具体做法往往是利用处于最紧贴边界的紧互对原型对产生一初始分界面,然后利用交遇区进行调整,这种调整属于局部性的调整。
在找到一组“交遇区”之后,将这些“交遇区”中的两类样本作为新的样本集,由它们产生分段线性判别函数。具体做法是:
步骤一: 产生初始超平面
首先由紧互对原型对集合中最近的一对,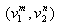 产生一个初始决策面的方程。例如可由这两个原型的垂直平分平面作为初始界面,表示成H1;
产生一个初始决策面的方程。例如可由这两个原型的垂直平分平面作为初始界面,表示成H1;
步骤二: 初始决策面最佳化
确定H1能正确分类的所有紧互对原型对,并由这些原型对中的样本组成局部训练的样本集,按所使用的准则设计出线性决策面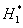 ,该决策面对现有局部样本集来说是最佳的。对该H1决策面又可找出它能正确分类的所有紧互对原型对。如果
,该决策面对现有局部样本集来说是最佳的。对该H1决策面又可找出它能正确分类的所有紧互对原型对。如果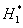 与 与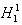 的分类效果相同,则 的分类效果相同,则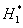 不需再调整,否则由 不需再调整,否则由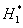 作为初始决策面重复上述过程,直到所包罗的局部训练样本集不再发生变化为止。 作为初始决策面重复上述过程,直到所包罗的局部训练样本集不再发生变化为止。
步骤三: 新决策面的产生与最佳化
在找到一个最佳的决策面段后,将相应的局部训练样本从原紧互对原型对集合中撤走,然后在剩下的紧互对原型对集合重复上述步骤,产生另一个超平面分界面,如此重复下去直到所有紧互对原型对都被处理完毕,得到一系列超平面,组成分段线性分类器。
3.3.4.3 分段线性分类器检验一个决策规则的确定
在使用上述方法得到一组超平面作为分段线性分类器的分界面后,仅对交遇区的样本集进行性能检测有时不能发现存在的问题,需要使用全体样本对其进行性能检验,观察其能否对全体样本作出合理的划分。例如图3.16(a)所示样本利用局部训练法产生了H1与H2两个超平面,将整个特征空间划分成R1、R2与R3三个决策域。在R1域中第二类样本占绝大多数,因此R1可作为第二类样本ω2的决策域,错误率不会很大。同样在R3域中ω1占大多数,R32可作为ω1的决策域。问题出在R2域。在R2域中ω1与ω2两类样本均占相当比例,因此不能简单地将其确定为哪一类的一个决策域,而需要对其进行进一步划分。下面说明使用全体样本进行检验及改进的具体作法。
如果现有的决策界面数为m,每个决策超平面的增广权向量为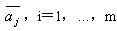 ,那么每一个样本yj处在哪个区域,可用它们与这些增广权向量
,那么每一个样本yj处在哪个区域,可用它们与这些增广权向量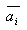 的内积符号表示。为了统计这些内积符号的总效果,可定义一个由样本Xj(用增广样本向量yj表示)决策的m维向量 的内积符号表示。为了统计这些内积符号的总效果,可定义一个由样本Xj(用增广样本向量yj表示)决策的m维向量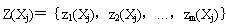 ,其中 ,其中
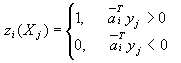 (3-58) (3-58)
因此处在同一区域的所有样本都有同样的向量值。例如图3.16(b)中,处在R1域中所有样本的m维向量(m=2)为Z={1,1};而在R2或中的样本具有Z={0,1};R3域中则为{0,0}。这样一来,全体样本将被划分若干子集,最大可能的子集数为2m个。每个子集都可能包含两个类别的训练样本,但在每个子集中两类样本分布的不同,将作为划分与改进决策域的依据。我们用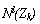 表示在第k个子集中第l类训练样本的个数,k=1,…,2m,l=1,2,并用一个比值函数 表示在第k个子集中第l类训练样本的个数,k=1,…,2m,l=1,2,并用一个比值函数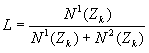 表示每个子集中ω1类样本所占比例,根据L值及N1(ZK)与N2(ZK)这三个数据,可对各个区域作相应决定:
表示每个子集中ω1类样本所占比例,根据L值及N1(ZK)与N2(ZK)这三个数据,可对各个区域作相应决定:
1 如果L>>1/2,则ZK区域为ω1的决策域;
2 如果L<<1/2,则ZK区域为ω2的决策域;
3 如果L≈1/2,以及N1(ZK)、N2(ZK)很小,则对ZK内样本可作拒绝决策;
4 如果L≈1/2,但N1(ZK)与N2(ZK)数量不可忽略,则对此区域,用该子集的样本再次进行局部训练法训练,以获得其进一步划分。重复上述过程,直至对所有区域都能合理地确定为哪一类的决策域,或拒识区域为止。
|