要弄懂这种错误修正算法的原理,首先要弄清值 相比较的含义。我们知道ai与aj代表两类增广权向量,y则代表规范化的增广权向量,这在感知准则函数中已定义过。
相比较的含义。我们知道ai与aj代表两类增广权向量,y则代表规范化的增广权向量,这在感知准则函数中已定义过。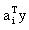 是ai向量与y向量的点积, 是ai向量与y向量的点积,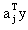 是aj向量与y向量的点积。一般来说点积值比较大则表示这两个向量在方向上比较一致,换句话说向量间的夹角较小。如果某一类样本比较分散,但是能用若干个增广权向量表示,使同一类规范化增广样本向量能够做到与代表自己一类的增广权向量的点积的最大值比,与其它类增广权向量的点积值要大,就可以做到正确分类。因此这种算法就是要用错误提供的信息进行叠代修正。所以它对每类样本集进行具体划分,而希望能知道每类所需的增广权向量数目。当然,实际上,该数目也可以在计算过程中按分类效果调整。 是aj向量与y向量的点积。一般来说点积值比较大则表示这两个向量在方向上比较一致,换句话说向量间的夹角较小。如果某一类样本比较分散,但是能用若干个增广权向量表示,使同一类规范化增广样本向量能够做到与代表自己一类的增广权向量的点积的最大值比,与其它类增广权向量的点积值要大,就可以做到正确分类。因此这种算法就是要用错误提供的信息进行叠代修正。所以它对每类样本集进行具体划分,而希望能知道每类所需的增广权向量数目。当然,实际上,该数目也可以在计算过程中按分类效果调整。
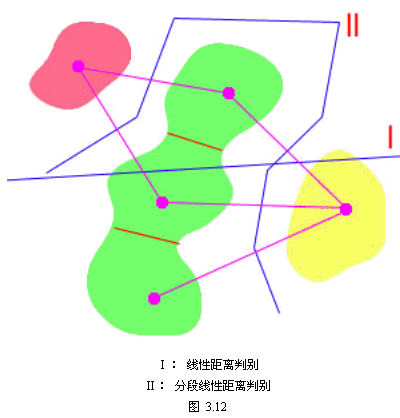
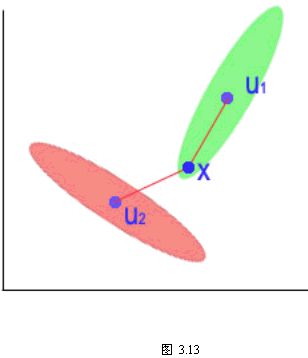
当每类的子类数目已知时,可以采用假设初始权向量,然后由样本提供的错误率信息进行迭代修正,直至收敛。该算法的基本要点是:
|
|
对每个类别的子类赋予一初始增广权向量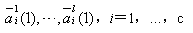 ,其中括号中的数目表示迭代次数。然后对每次迭代所得增广权向量用样本去检测,如发生错误分类,则利用错误分类的信息进行修正。其做法是: ,其中括号中的数目表示迭代次数。然后对每次迭代所得增广权向量用样本去检测,如发生错误分类,则利用错误分类的信息进行修正。其做法是:
先将某一j类的增广样本向量yj,与该类所有增广权向量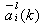 求内积 求内积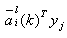 ,找到其中的最大值 ,找到其中的最大值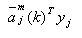
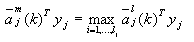 (3-53) (3-53)
另一方面将该yj与其它类(如i类)的权向量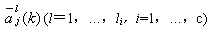 求内积,并将这些内积值与 求内积,并将这些内积值与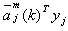 作比较,若 作比较,若
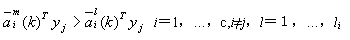 (3-54) (3-54)
则表明权向量组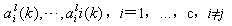 ,不影响yi的正确分类,因此由yi所提供的信息表明这些权向量都不再需要修改。但是如果存在某个或几个子类不满足上述条件,譬如某个子类 ,不影响yi的正确分类,因此由yi所提供的信息表明这些权向量都不再需要修改。但是如果存在某个或几个子类不满足上述条件,譬如某个子类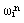 的现有权向量 的现有权向量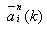 使得 使得
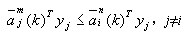 (3-55) (3-55)
这表明yj将错分类,而有关权向量需要修正。此时首先找到导致yj错分类的所有权向量中具有与yj内积最大值的权向量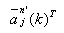
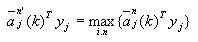 (3-56) (3-56)
接着对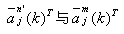 作相应修正 作相应修正

然后利用权向量的新值重复以上过程,直到收敛或迫使其收敛。这种算法在样本确实能被分段线性判别函数正确划分的条件下是收敛的。但当该条件不满足时,则需逐步减小ρk的数值,迫使其“收敛”,显然会有相应的错误率存在。
|
|


