| 对实际的模式识别问题来说,各类在特征空间中的分布往往比较复杂,因此无法用线性分类函数得到好的效果。这就必须使用非线性的分类方法。在对待非线性判别分类问题,,提到的三种不同的方法。传统的模式识别技术,则侧重于使用分段线性判别函数,因此基本上是沿用了线性判别函数的方法。这在3.3.1到3.3.4中讨论。3.3.2的错误修正法是对感知准则函数的扩展,但人工神经元网络如多层感知器等网络能够实用非常复杂的非线性分类,以及非线性函数拟和,非线性映射等,这将在人工神经元网络这一章讨论。支持向量机则提出了一种基于特征映射的方法,也就是使用某种映射,使本来在原特征空间必须使用非线性分类技术才能解决的问题,映射到一个新的空间以后,
使线性分类技术能继续使用。 3.3.1 非线性判别函数与分段线性判别函数 |
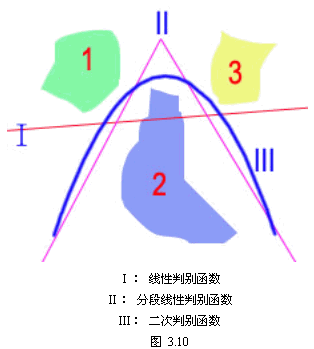 |
| 由于样本在特征空间分布的复杂性,许多情况下采用线性判别函数不能取得满意的分类效果。例如对图3.10所示两类物体在二维特征空间的分布,采用线性判别函数就无法取得满意的分类效果。在这种情况下,可以采用分段线性判别或二次函数判别等方法,效果就会好得多。与一般超曲面相比,分段线性判别函数是最为简单的形式,是非线性判别函数情况下最为常用的形式。除此之外二次判别函数是除线性及分段线性外最简单的形式。以下只讨论有关分段线性判别函数设计中的一些基本问题。 与线性判别函数相比,分段线性判别函数设计中首先要解决的问题是分段线性判别函数的分段段数问题,显然这是一个与样本集分布有关的问题。分段段数过少,就如图3.10的例子中用一个线性判别函数(段数为1)的情况,其分类效果必然要差;但段数又要尽可能少,以免分类判别函数过于复杂,增加分类决策的计算量。在有些实际的分类问题中,同一类样本可以用若干个子类来描述,这些子类的数目就可作为确定分段段数的依据。但多数情况下样本分布及合适子类划分并不知道,则往往需要采用一种聚类的方法(在第五章中讨论),设法将样本划分成相对密集的子类,然后用各种方法设计各段判别函数。由于在后面章节要讨论聚类问题,这一章主要讨论在样本分布及子类划分大体已定的情况下,设计分段线性判别函数的问题,着重讨论几种典型的设计原理。 分段线性判别函数的一般形式可定义为: 其中 如果 其中 则决策 至于分类的决策面方程取决于相邻的决策域,如第i类的第n个子类与第j类的第m个子类相邻,则由它们共同决定的决策面方程为 当每一类的样本数据在特征空间中的分布呈复杂修正时,使用线性判别函数就会产生很差的效果,如果能将它们分割成子集,而每个子集在空间聚集成团,那么子集与子集的线性划分就可以取得比较好的效果。因此分段线性判别的主要问题是如何对数据划分成子集的问题,这是第五章着重讨论的内容。 |