二、线性分类器 　　决策面为超平面的分类器称为线性分类器。 　　有不止一种正态分布概率模型，可使最小错误率贝叶斯决策的决策面具有超平面形式。这里我们讨论两种情况。 　　(1)Σi=σ2I i=1,…，c 　　这种情况与上一种情况不同之处在于并不要求各类的先验概率相等这个条件。在这种情况下，判别函数可从(2-48)简化为 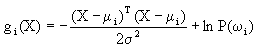　　　　　(2-42) 　　(2-42)是X的二次函数，但是由于二项XTX与类别号i无关，因此判别函数可进一步简化成 　　　　　　　(2-43)　 　　其中 　　 　　　　　　　　(2-44) 　　　　　　(2-45)　 　　可见判别函数为一线性函数。根据决策面方程gi(X)－gi(X)＝0可有 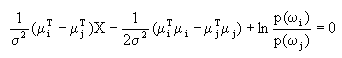　　　　　　(2-46) 　　利用及 　　代入(2-46)并整理，可得 　　WT(X－X0)＝0 (2-47) 　　其中 　　W＝μi-μj 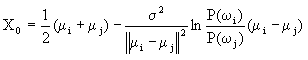　　　　　　(2-48) 　　由(2-47)与(2-48)式可以看出，决策面为一超平面，其法线方向为(μi－μj)，当P(ωi)＝P(ωj)时该超平面过(μi+μj)/2点，在二维情况下，就是过μi与μj连线的垂直平分线，如图2.8(a)所示。当P(ωi)≠P(ωj)时，该超平面的位置要向远离先验概率大的方向偏，但超平面方向不变。 　　从上面讨论的最小距离分类器与线性分类器中可以看出，这两者都是线性分类器，最小距离分类器是线性分类器的一个特例。另一点是最小距离分类器在正态分布情况下，是按超球体分布以及先验概率相等的前提下，才体现最小错误率的。最小距离分类器的思想在分类器设计中是一种较常用的方法。以上分析表明，只有在一定条件下，最小距离分类器同时又是最小错误率分类器。 　　实际上，最小距离分类器的概念是分类器中是最常用的，因为它体现了基于最相似性的原则，即被分类事物与哪一种作为标准的事物相像，就判为该类这一原则。在这一节的分析则说明了什么条件下最小距离分类器同时实现了最小错误率。在正态分布条件下，一是正态分布的协方差矩阵为单位矩阵，因此等概率密度点轨迹对应于欧氏距离为常数；另一是先验概率要相等，这一点在解实际问题中往往加以忽略，因为先验概率难以得到。 　　(2)Σi=Σ 　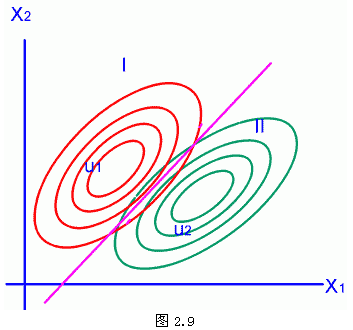　能采用线性分类器的另一种简单情况是Σi＝Σ，即各类的协方差矩阵都相同。从几何上看，这相当于各类样本具有同样概率密度函数的点的轨迹是同样大小和形状的超椭球面。但不同类样本的超椭球面的中心由类均值μi决定。图2.9表示在二维特征空间的情况，此时超椭球面是二维空间的椭圆。 　　在Σi＝Σ，i=1,…，c的条件下，由于Σ与类别号i无关，因此判别函数可从(2-37)简化成 　　(2-49) 　　如果c类先验概率都相等，则(2-49)可进一步简化为 　　(2-50) 　　(2-50)的右边正是前面提到的Mahalanobis距离的平方。因此这时的决策规则为：计算X到每类均值μi的Mahalanobis距离平方r2，把它归于r２最小的类别。为了确定先验概率不等条件下的决策面方程，可以展开(2-57)并忽略与i无关的XＴΣ－１X项，经整理可得 　　 (2-51) 　　其中 　　(2-52) 　　(2-53) 　　由(2-51)可以看出决策面方程也是线性方程，决策面是超平面。如果第i类与第j类的决策域在特征空间中相邻，则这两者之间的决策面方程为 　　gi(X)－gj(X)＝0 　　即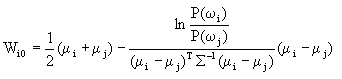(2-54) 　　其中(2-55) 　　　　　(2-56) 　　如果将(2-55)、(2-56)与(2-48)的两个式子相比较，可以发现这两对式子很相近，只是(2-48)中的欧氏距离‖μi-μj‖２在(2-56)中由Mahalanobis距离的平方所取代。另一点是W在式(2-55)中多了一个Σ－１因子。因此可以作出相应结论：当P(ωi)＝P(ωj)时，其相应的决策面超平面过均值向量连线的中点；但当先验概率不等时，超平面朝远离先验概率大的方向移动。与上一小节不同的是，一般情况下该超平面不与两均值向量的连线正交。 　　图2.9画出在二维特征空间先验概率相等的情况。 　　到此为止将上面讨论的情况总结一下, 以有利于加深理解。以上几种情况都是线形分类器的情况，也就是用线形函数作为判别函数，或分界面方程是线性。在正态分布条件下，基于最小错误率贝叶斯决策只要能做到两类协方差矩阵是一样的，那么无论先验概率相等不相等，都可以用线性分界面实现。而最小欧氏距离分类器则要求正态分布协方差矩阵为单位阵，先验概率相等。反过来说，如果希望用线性分类器实现错分类少的分类，则两类用正态分布近似时，应要求其协方差矩阵相似，先验概率相近才行。当然如果两类分布分得很开，没有什么重叠，也可做到错分率很小。与下一节讨论的情况相比，可以看到为了实现错分率小，分界面类型就要比线性函数类型复杂了，在正态分布条件下，一般是超二次曲面。