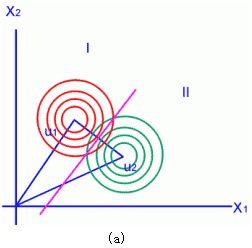
在下面的讨论中采用(2-3)式表示的决策规则，即 　　如果 　　则X∈ωi 　　因此判别函数为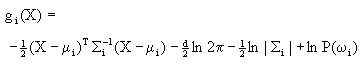，其中是多元正态分布，可表示成。考虑到正态分布函数是指数函数形式，判别函数采用对数形式则更为方便，因此判别函数可写成： 　　(2-37) 　　而相应的决策面方程为 　　 　　即 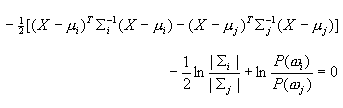　　　　　(2-38) 一、最小距离分类器情况 　　在正态分布的某一种特殊情况下，最小错误率贝叶斯分类器可演化成最小距离分类器。最小距离分类器的定义是，每个样本以它到每类样本均值的欧氏距离的最小值确定其分类，即 　　如果 　　则X∈ωi (2-39) 　　样本分布满足以下正态分布条件时，最小错误分类器与(2-39)表示的决策规则相当； 　　 　　其中I是d×d维单位矩阵，即 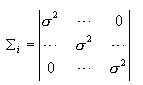　　 　　以上条件表明，c类样本都以半径相等的超球面形状分布在特征空间内，且具有相等的先验概率。图2.8(a)表示一个在二维特征空间中满足上述条件的两类别问题示意图，图中两类分布为两个相同的同心园，图中μ1与μ2为其圆心。 　　在这种条件下，由于|Σ|＝σ2d及Σi-1=σ2I，代入(2-37)得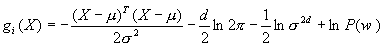 　　　　(2-40) 　　由于决策是根据各判别函数之间的大小，因而在(2-48)中一些与类别无关的项可以忽略，再加上先验概率相等这个条件，判别函数可简化成 　　　　(2-41) 　　由此可见，在这种条件下，最小欧氏距离是决定分类的准则。图2.8(a)表示了两类别情况下μ1与μ2连线的垂直平分线是其决策面，图2.8(b)则画出多类别的情况，它们分别是相邻区域的垂直平分线组合而成。 　　前面我们曾经提到过分类的两种基本方法中的一种——模板匹配，最小距离分类器就可看作模板匹配。每个类有一个典型样本(即均值向量)，称为模板，而待分类样本X只要按欧氏距离计算与哪个模板最相似(欧氏距离最短)即可作决定。