2.多元正态分布的性质
　　(1)参数μ与Σ对分布具有决定性。这一点与单变量时是相似的，记作p(X)～N(μ，Σ)。
　　(2)等密度点分布在超椭球面上。
　　由于(2-32)是指数函数，因此等密度点对应：
　　(x－μ)^ＴΣ^－１(x－μ)＝常数 (2-35)
　　在二维情况下，(2-35)的解是一个椭圆轨迹，其长短轴方向由Σ协方差矩阵的特征向量决定，在三维时则是一个椭球面，超过三维则是超椭球面，主轴方向由协方差矩阵的特征向量决定，各主轴的长度则与相应的特征值成正比。
　　在数理统计中把(X-μ)^ＴΣ^－１(X-μ)称为向量X到向量μ的Mahalanobis距离的平方，即
　　r₂＝(x－μ)^ＴΣ^－１(x－μ) (2-36)
　　按此定义多元正态分布等密度点X的轨迹是到μ的Mahalanolbis距离为常数的超椭球面。
　　(2－43)式在二维时表示一个椭圆，在三维表示椭球，在高维是表示超椭球，这是一个二次型问题，在线性代数中学过，为了复习，读者可　　以用二维的例子来计算。简便起见，设(2-35)式中 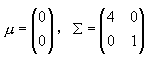。试求满足此条件的曲线。
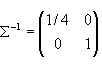　　( ，故得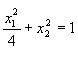，为一个椭圆)
　　可将mahalanolbis距离与欧氏距离作比较，前者是一个椭圆，而后者则是圆。请问可以用(2－43)表示欧氏距离吗？Σ＝？
　　(Σ=I 是单位矩阵)
　　(3)多元正态分布的离散程度由参数|Σ|^１／２决定，这与单变量时由标准差σ决定是对应一致的。
　　(4)不相关性等价于独立性。在数理统计中一般情况下，两个随机变量x_i与x_j之间不相关，并不意味着它们之间一定独立。不相关只表明E[x_ix_j]＝E[x_i]·E[x_j]，即两变量乘积的期望值等于这两变量期望值之乘积，而只有p(x_i,x_j)＝p(x_i)p(x_j)，即两变量的联合密度函数等于两者概率密度函数的乘积，这两个随机变量才是独立的。但反过来相互独立的随机变量，它们之间也是不相关的。然而对多元正态分布的任意两个分量x_i与x_j而言，如果x_i与x_j不相关，则它们之间也一定是独立的，也就是说正态分布中不相关性等价于独立性。
　　(5)边缘分布和条件分布的正态性。
　　多元正态分布的边缘分布和条件分布仍然是正态分布。这就是说多元正态的随机向量，就其每个分量单独的分布而言，也是正态分布的。另一方面，对某个分量或若干个分量保持常数的条件下样本的分布也仍然是正态的。
　　(6)线性变换的正态性。这是指多元正态分布的随机向量的线性变换仍然是多元正态分布的随机向量。如果设X[x₁，x₂，…，x_d]^Ｔ，是具有均值向量μ，正定协方差矩阵为Σ的正态随机向量，现对X作线性变换得Y＝AX，其中A是非奇异的线性变换矩阵，则Y也是正态分布的，它的均值向量为Aμ，而协方差矩阵为AΣA^Ｔ。这表明经线性变换后，原正态分布的样本可变为另一参数不同的正态分布样本。同时由于协方差矩阵Σ是对称矩阵，因此总可以找到某个线性变换A，使变换后的协方差矩阵AΣA^Ｔ成为对角矩阵，这就意味着在某一个新的坐标系统中，可以做到使各分量之间是相互独立的。这一性质对解决某些模式识别问题有重要意义。
　　(7)线性组合的正态性。这是指多元正态分布的随机向量，在经过线性组合后得到的一维随机变量也是正态分布的。用式子表示为，若X＝[x₁，…，x_d]^Ｔ，α是与其同维的某个向量，如用α对X实行线性组合得Y＝α^Ｔx，则Y的分布仍然是正态的。
　　以上列举了正态分布随机向量的一些性质，在下面讨论正态情况下的贝叶斯决策中将会用到其中一些性质。