本节中只给出有关定义及性质，一般情况下不讨论如何证明。 一、单变量正态分布 　　 单变量正态分布概率密度函数定义为 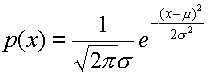　　(2－29) 　　式中μ表示随机变量x的数学期望，σ2为其方差，而σ则称为标准差。 　　(2-30) 　　(2-31) 　　(2-29)表明单变量正态分布概率密度函数p(x)完全可由μ与σ2两个参数确定，常记作N(μ，σ2)。正态分布的样本主要集中分布在其均值附近，其分散程度可用标准差来衡量，σ愈大分散程度也越大。从正态分布的总体中抽取样本，约有95%的样本都落在区间(μ－2σ，μ+2σ)内。 　　为了加深对正态分布的理解，对正态分布再进一步讨论一下。 　　首先正态分布是指一个随机实数度量值在整个实数域上的分布规律。因此它属于概率密度函数类，不是我们所讨论的先验概率P(ωi)，也不是后验概率P(ωi|X)，而是p(x|ωi)。式(2-37)用p(x)表示，是因为通用公式，如具体到我们的情况，可将(2-37)具体化，则 　　 　　其中ωi, σi分别是对(2-29)中ω及σ的具体化。 　　请思考一下，正态分布(又称高斯分布)以x为横轴，y为纵轴画出来是什么样子？有没有最高点？最高点的x坐标是什么？σ的大小对你所画的图有什么影响？如果有两种高斯分布μ1=μ2，σ1>σ2，你能将它们画在一起吗？两者有什么不同？均值μ和标准差σ两个概念十分重要，一定要弄清楚。