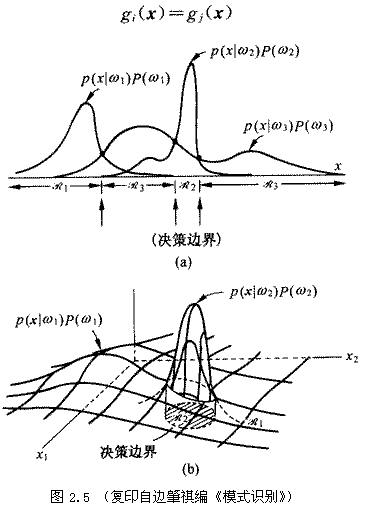
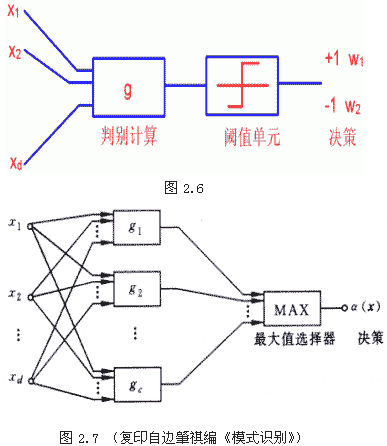
例如在两类别问题中，按最小错误率作决策时，决策规则的一种形式是 　　 ，否则 　　则相应的判别函数就是 　　gi(X)＝P(ωi|X), i=1,2 　　而决策面方程则可写成 　　g1(X)＝g2(X) 　　此时决策规则也可以写成用判别函数表示的形式 　　如果gi(X)＞gj(X) i,j=1,2 且 i≠j 　　则X∈ωi，否则 　　至于多类别情况，则对应于一种决策规则要定义一组判别函数 　　gi(X)， i=1,2,…，c 　　而决策规则可表示成 　　如果，则将X归于ωi类； 　　多类别情况下的决策面方程比两类问题复杂，并且只有在特征空间中具有相邻关系的决策域的边界面才是有意义的决策面。当ωi的决策域与ωj的决策域相邻时，以下关系决定了相应的决策面gi(X)＝gj(X) 　　此外，决策面是一种统称，当特征空间只是一维时，一个决策面实际上只是一个点。在二维特征空间里，决策面是一条曲线。三维则是一曲面，超过三维的空间，决策面是一个超曲面。图2.5(a)表示了一个三类别问题用一维特征空间时的所有决策边界，而图2.5(b)则表示了相应的二维特征空间中的决策边界。 　　在讨论了判别函数等概念后，设计分类器的任务就清楚了。分类器可以用软件或硬件实现。图2.6表示了两类别问题分类器的框图，而图2.7则表示了多类别分类器的结构框图。两者主要的不同在于多类别情况需有一个求最大值的环节，在图2.7中用MAX表示，而两类情况则可简化为正负号判别器(阈值单元)。   　　分类器设计除了确定结构框图外，问题主要集中在判别函数的选择，使用最小风险决策时合理的损失函数的确定。此外贝叶斯决策理论都是基于统计分布确定的情况下的计算，而统计参数的确定恰恰是最困难的问题。如果要按贝叶斯决策方法设计分类器，就必须设法获得必需的统计参数，这个问题在此网络版上不再讨论，可参看《模式识别基本教程》。 　　前面讨论的Bayes决策理论其实是很简单的，对特征空间任一点X只要能确定落在该点的样本X属于哪一种类的可能性大，就将这点划分到这类的决策域。问题是后验概率P(ωi|X)要通过先验概率和类概率密度函数计算。因为Bayes决策是一种通用方法，它只在原理上讲特征空间中符合什么条件才能作为哪一类决策域，而我们希望能把决策域用简便的方式，最好是函数形式划分出来，直接计算判别函数就方便了。显然具体的决策域划分与样本的概率分布有关。下面结合正态分布概率密度函数进行讨论，在讨论结束时我们会发现从中可以得到不少启示。