如令
由于先验概率P(ω1)与P(ω2)在具体问题中往往是确定的,因此一般称P1(e),P2(e)为两类错误率。实际中,有时要求将其中某一类错误率限制在某个常数之下而使另一类错误率尽可能小。例如在癌细胞识别中,希望将异常细胞错判的概率P2(e)限制在很小的值,如P2(e)=ε0为一个很小的常数,同时又使P1(e)尽可能小。
这种决策要求可看成是在P2(e)=ε0条件下,求P1(e)极小值的条件极值问题,因此可以用求条件极值的拉格朗日乘子法解决。为此我们写出如下算式
其中λ为拉格朗日乘子,目的是求γ的极小值。按定义
其中R1与R2分别是ω1与ω2的决策域,而R1与R2组成整个特征空间R,且彼此互不交迭。因此如果被识别样本X落入R1中,就被判定为ω1,反之属ω2。由于R1与R2不相交并组成整个特征空间,应有
将式(2-21),(2-22)代入(2-20),并考虑到(2-23)可得
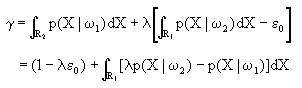 (2-24)
(2-24)将(2-24)式分别对X和λ求导,并令
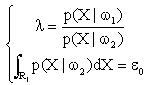 (2-25)、(2-26)
(2-25)、(2-26)(2-25)与(2-26)的方程式就决定了这样一个分界面λ,它使P2(e)=ε0,同时又在该条件下使P1(e)尽可能小。该分界面上X值具有这样一个特点,即它们的两类条件密度函数之比是一个常数,该比值就是拉格朗日乘子。
这种决策规则可写成:
如果
或
如果
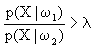 ,则
,则这种在限定某一类错误为常数而使另一类错误率最小的决策也称Neyman-Pearson决策规则。如果将(2-28)与最小错误率决策规则(2-24)相对比,可以看出Neyman-Pearson决策规则也是以似然比为基础的,但两者所使用的阈值不同。最小错误率决策使用
管(2-25)与(2-26)提供了该种决策的决策面方程,但在高维时,即d较大时,直接求解是不容易的。一般可利用P2(e)与λ值之间存在的单调函数关系,采用选择一些λ值的试探法,最终找到一合适的λ值,既能使P2(e)=ε0条件满足,又能使P1(e)尽可能小。