例2.2
在例2.1条件的基础上,并且已知λ11=0,(λ11表示λ(α1|ω1)的简写),λ12=6,λ21=1,λ22=0,按最小风险贝叶斯决策进行分类。
解:已知条件为
P(ω1)=0.9, P(ω12)=0.1
p(X|ω1)=0.2, p(X|ω12)=0.r
λ11=0, λ12=6, λ21=1, λ22=0
根据2.1的计算结果可知后验概率为
P(ω1|X)=0.818, P(ω12|X)=0.182
再按式(2-14)计算出条件风险
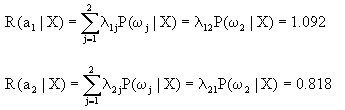
由于R(α1|X)>R(α2|X)
即决策为ω12的条件风险小于决策为ω1的条件风险,因此应采取决策行动α2,即判待识别的细胞X为ω12类——异常细胞。
将本例与例2.1相对比,其分类结果正好相反,这是因为影响决策结果的因素又多了一个“损失”。由于两类错误决策所造成的损失相差很悬殊,因此“损失”在这里起了主导作用。
从以上讨论可以看出,正确制订损失函数值,是基于最小风险的贝叶斯决策方法在实际中使用的一个关键问题。而实际中列出合适的决策表并不是一件容易的事,需根据所研究的具体问题,分析错误决策造成损失的严重程度,与有关专家共同商讨来确定。
最后我们再讨论一下上面两种决策方法之间的关系,设损失函数为
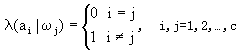 ,
(2-17) ,
(2-17)
式中假定对C类只有C个决策,即不考虑“拒绝”等其它情况,(2-17)表明,当作出正确决策(即i=j)时没有损失,而对于任何错误决策,其损失均为1。这样定义的损失函数称为0—1损失函数。
根据(2-14)式条件风险为
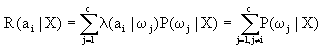 (2-18) (2-18)
而 也恰恰是将X判为ω1i时的错误概率。因此基于最小风险的贝叶斯决策结果,在0—1损失函数情况下,也就是基于最小错误概率的贝叶斯决策结果。由此可见,最小错误率贝叶斯决策就是在0—1损失函数条件下的最小风险贝叶斯决策。换句话说,前者是后者的特例。 也恰恰是将X判为ω1i时的错误概率。因此基于最小风险的贝叶斯决策结果,在0—1损失函数情况下,也就是基于最小错误概率的贝叶斯决策结果。由此可见,最小错误率贝叶斯决策就是在0—1损失函数条件下的最小风险贝叶斯决策。换句话说,前者是后者的特例。
实际上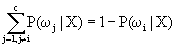 ,因此,当 ,因此,当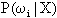 最大时
最大时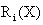 最小。 它与基于最小错误率的贝叶斯决策的判据是一样的。
最小。 它与基于最小错误率的贝叶斯决策的判据是一样的。
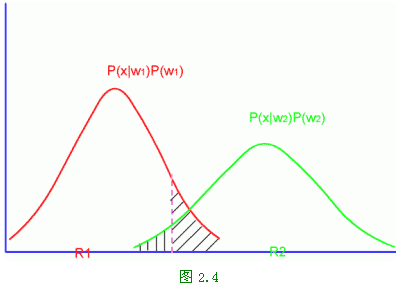
如果我们只考虑两类别问题,并只有一维特征向量的情况,我们可以画出一张与图2.3类似的图2.4,用来表示最小风险贝叶斯决策方法的分类结果。与图2.3不同的是,R1与R2两个区域的分界线不再是t,而是向左移了一段距离,这是由于损失函数λ12比λ21大所造成(可以假设λ11=λ22=0),在发生位移这一区域内,尽管P(x|ω1)P(ω1)>P(x|ω12)P(ω12),但是为了减少将ω12错判为ω1所带来的严重损失,在P(x|ω12)P(ω12)尚不很小的情况下,使将ω12类样本错判为ω1的可能性减小,以减小决策所承担的风险。当然平均错误率则明显增大了。
|
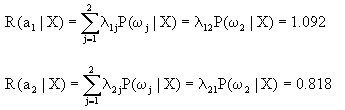
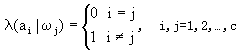 ,
(2-17)
,
(2-17)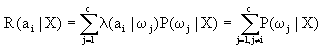 (2-18)
(2-18)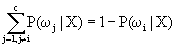 ,因此,当
,因此,当