在讨论基于风险的决策方法的具体内容之前，让我们首先回顾一下上一节讨论的基于最小错误概率的决策方法。从式(2-10)可以看出，在分类时所作的判决(称之为决策)单纯取决于观测值X对各类(也称自然状态)的后验概率中之最大值，因而也就无法估计作出错误决策所带来的损失。为此不妨将作出判决的依据从单纯考虑后验概率最大值，改为对该观测值X条件下各状态后验概率求加权和的方式，表示成
(2-13)
其中
表示观测样本X实属类别j,而被判为状态i时所造成的损失，Ri则表示了观测值X被判为i类时损失的均值。如果我们希望尽可能避免将某状态ωj,错判为状态ωi,则可将相应的
值选择得大些，以表明损失的严重性。加权和Ri用来衡量观测样本X被判为状态ωi所需承担的风险。而究竟将X判为何类则应依据所有Ri,(i=1,…,c)中的最小值，即最小风险来定。
我们再从另一角度把这个问题说清楚。我们见到一个病理切片X，要确定其中有没有癌细胞(用ω1表示正常，ω2表示异常)，则P(ω1|X)与P(ω2|X)分别表示了两种可能性的大小。如果X确实是癌细胞(ω2)，但被判作正常(ω1)，则会有损失，这种损失用
表示，X确实是正常(ω1)，却被判定为异常(ω2)，则损失表示成
，另外为了使式子写的更方便，我们也可以定义
与
，是指正确判断也可有损失。那么把X判作ω1引进的损失应该与以及都有关，哪一个占主要成分，则取决于P(ω1|X)与P(ω2|X)。因此变成了一个加权和
同样将X判为ω2的风险就成为
此时作出哪一种决策就要看是R1(X)小还是R2(X)小了，这就是基于最小风险的贝叶斯决策的基本出发点。有关该例的数值例子在例2.2。
以上讨论是为了说明这种方法的概念。下面我们给出一些确切的定义。
(1)自然状态与状态空间。其中自然状态是指待识别对象的类别，而状态空间Ω则是由所有自然状态所组成的空间，
Ω={ω1，ω2，…，ωc}
(2)决策与决策空间。在决策论中，对分类问题所作的判决，称之为决策，由所有决策组成的空间称为决策空间。决策不仅包括根据观测值将样本划归哪一类别(状态)，还可包括其它决策，如“拒绝”等，因此决策空间内决策总数a可以不等于类别数c,表示成
(3)损失函数λ(αi|ωj)(或写成λ(αi,ωj))。这就是前面我们引用过的。它明确表示对自然状态ωj，作出决策αi时所造成的损失。
(4)观测值X条件下的期望损失R(αi|X),
,i=1,2,…,a (2-14)
这就是前面引用的符号Ri，也称为条件风险。
与式(2-10)类似，最小风险贝叶斯决策规则可写成：
如果
,则α=αk (2-15)
但与(2-10)式不同的是，这里计算的是最小值。
与上一小节中基于最小错误概率的决策方法中所引用的平均错误率P(e)相类似，在这里引入一个期望风险R，
(2-16)
它表示对所有X取值所作的决策α(X)所带来的平均风险。与上一节证明基于最小错误概率的贝叶斯决策方法相类似，当所采取的每一个决策都使其条件风险最小，则对所有的X所作的决策，其期望风险也必然最小。
对于实际问题，最小风险贝叶斯决策可按下列步骤进行：
(1)在已知P(ωi)，P(X|ωi)，i=1,…，c及给出待识别的X的情况下，根据贝叶斯公式计算出后验概率：
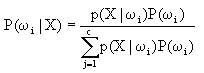j=1,…，x
(2)利用计算出的后验概率及决策表，按式(2-14)计算出采取αi,i=1,…，a的条件风险
,i=1,2,…,a
(3)对(2)中得到的a个条件风险值R(αi|X),i=1,…，a进行比较，找出使条件风险最小的决策αk，即
则αk就是最小风险贝叶斯决策。