由于统计判别方法是基于统计参数作出决策，因此错误率也只能从平均的意义上讲，表示为在观测值可能取值的整个范围内错识率的均值。在连续条件下，平均错误率，以P(e)表示，应有 　　(2-6) 　　其中p(e,x)表示错误率为e观测值为x的联合概率密度，P(e|x)是观测值为x时的条件错误概率密度函数，P(x)为x值出现的概率，而积分运算则表示为在整个d维特征空间上的总和。在此一维情况下，x取从－∞到+∞的整个范围。 　　在两类别问题中，按(2-2)式给出的决策规则，当P(w2|x)＞p(w1|x)时决策为w2。显然这个决策意味着，对观测值x有P(w1|x)概率的错误率。例如在上例中所作的w1决策，实际上包含有P(w2|x)=0.182的错误概率。在两类别的情况下，可以将p(e|x)表示成当 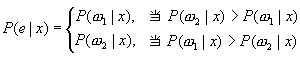　　(2-7) 　　如果我们把作出w1决策的所有观测值区域称为R1，则在R1区内的每个x值，条件错误概率为p(w2|x)。另一个区R2中的x,条件错误概率为p(w1|x)。因此平均错误率P(e)可表示成 　　(2-8) 　　由于在R1区内任一个x值都有P(w2|x)＜P(w1|x)，同样在R2区内任一个x值都有P(w1|x)＜P(w2|x)错误率在每个x值处都取小者，因而平均错误率P(e)也必然达到最小，这就证明了按(2-2)式作出的决策，其平均错误率为最小。 　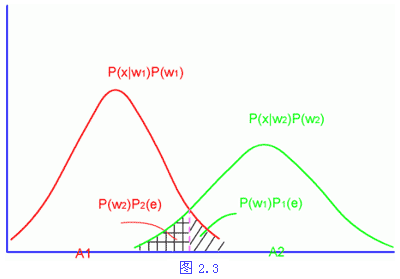　为了形象地说明以上证明，图2.3表示了在某种概率分布下R1与R2区的分布情况，该图分别画出p(x｜ω1)P(ω1)及p(x｜ω2)P(ω2)的分布情况，由于P(e)也可以(2-8)式写成 　　(2-9) 　　因此错误率为图中两个划线部分之和，显而易见只有这种划分才能使对应的错误率区域面积为最小。 　　以上讨论的是两类别问题情况，在C类别情况下，很容易写成相应的最小错误率贝叶斯决策规则： 　　如果 ,则 (2-10) 　　也可将其写成用先验概率与类条件概率密度相联系的形式，得： 　　如果 　　 (2-11) 　　至于计算多类别决策过程中的错误率，需把特征空间分割成R1，R2，…，Rc个区域，在每个区域Ri统计将所有其它类错误划为该区域对应的i类的概率，则每个区域共有c-1项错误率，总共有c(c-1)计算项，计算是很繁琐的。为此，可以改成计算平均正确分类概率P(c)即 　　(2-12) 　　由于上式中只有c项，计算要简单得多。然后通过式子P(e)=1-P(c)，就可计算出平均错误率。 　　例 应用贝叶斯决策的肤色提取 　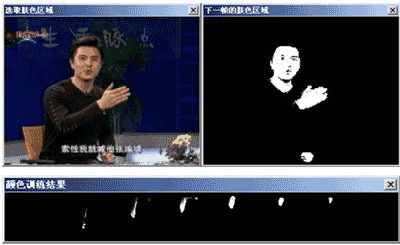　利用贝叶斯原理，可以建立简单的肤色模型，并用来从图像中提取手部、脸部肤色，进而得到人的身体姿势。 　　我们使用的方法是： 　　1．先在一副训练图象中手工描绘出肤色区域， 　　2．然后统计每种颜色点在肤色区域中出现的次数和在区域外出现的次数的比值，作为这种颜色是肤色的概率 　　3．这样就得到了一张查找表，表中的每个元素是这个点是肤色的概率。我们就得到了一个点是不是肤色的概率分布。以上的“颜色训练结果窗口”就是这样一张表的直观显示。实际表格是三维的(HSI颜色空间，32×32×8)把这个条形区域分成八块以后，每一块是个32×32的正方形，表示HS空间下的概率分布，颜色越亮，说明这种颜色是肤色的概率越大。 　　4．再加上域值限制之后，认为只有概率大于一定域值的才是肤色。 这样，对图中任意一点，查找表中对应的概率，就可以很快的知道它是不是肤色了。