下面举一数值例子。
　　例2.1
　　假设在某地区切片细胞中正常(ω₁)和异常(ω_２)两类的先验概率分别为P(ω₁)=0.9，P(ω₂)=0.1。现有一待识别细胞呈现出状态x，由其类条件概率密度分布曲线查得p(x|ω₁)=0.2，p(x|ω_２)=0.4，试对细胞x进行分类。
　　解：利用贝叶斯公式，分别计算出状态为x时ω₁与ω_２的后验概率
　　
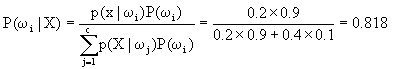
而
　　根据贝叶斯决策(2-2)则有
　　P(ω₁|x)＝0.818＞P(ω_２|x)＝0.0182
　　因此判定该细胞为正常细胞比较合理。请同学们用公式(2-3)与(2-5)计算，检查一下结果是否一样？
　　从这个例子可以看出，尽管类别ω_２呈现出状态x的条件概率要高于ω₁类呈现此状态的概率，但是考虑到P(ω₁)远大于P(ω_２)，因此状态x属于类别ω₁的可能性远比属于类别ω_２的可能性大。将该细胞判为正常在统计的意义上讲出错率要小得多。
　　为了帮助同学搞清楚一些基本概念，我们还要强调一下条件概率这个概念。我们举出两对概率，一对是P(ω₁|x)和P(ω_２|x)，另一对是P(x|ω₁)和P(x|ω₁)。从表面上看，只是条件符号两边的项对换了位置，但实质上却有很大区别。前一对是在同一条件x下，比较ω₁与ω₂出现的概率，如果我们只考虑两类ω₁和ω₂，则有P(ω₁|x)+P(ω₂|x)=1。而对两者进行数值上的比较，如P(ω₁|x)> P(ω₂|x)则可以下结论，在x条件下，事件ω₁出现的可能性大。
　　对后一对概率来说，与第一对完全不同，因为它们是在不同条件下讨论的问题因此比较两者没有意义，而且即使只有两类ω₁与ω₂，P(x|ω₁)+P(x|ω₁)≠1。这里要特别强调一点是P(x|ω₁)与P(x|ω₂)两者没有联系，都是指各自条件下出现x的可能性，不能仅因为前者比后者大，就认为x是第一类事物的可能性较大，只有考虑先验概率这一因素，才能决定x条件下，ω₁类还是ω₂类的可能性比较大。
　　另外大家可能觉得比较奇怪，为什么后验概率要利用Bayes公式从先验概率和类条件概率密度函数计算获得。这是因为计算概率都要拥有大量数据才行。在估计先验概率与类条件概率密度函数时都可搜集到大量样本，而对某一特定事件(如x)要搜集大量样本是不太容易的。因此只能借助Bayes公式来计算得到。
　　对基于最小错误率的贝叶斯决策来说，以后验概率值的大小作判据是最基本的方法，而其它形式的作用都基本相同，但使用时更方便些。
以上讨论的是在两类情况下基于最小错误概率的贝叶斯决策规则，下面需证明按这种规则进行分类确实使错误率为最小。下面仅以一维情况来证明，其结果并不难推广到多维的情况。