三、相似性度量 　　同类物体之所以属于同一类，在于它们的某些属性相似，因此可选择适当的度量方法检测出它们之间的相似性。人们也正是依据物体之间的相似程度将它们分类的。问题在于物体之间的相似性具有定性与不确定的性质，有时相似性与不相似性很难用明确的定量表示。而计算机却适合符号运算或数值计算。如果采用数值运算，则必须将赖以区别物体的相似性与不相似性用定量表示，这显然是非常困难的。如果采用符号运算来说明两个物体在什么方面相似与不相似，则往往也要从定量分析的基础得出定性的符号描述，这也正是许多实际模式识别问题的困难所在。 　　在特征空间中用特征向量描述样本的属性，就是把相似性度量用距度离量表示。在找到合适的特征空间情况下，同类样本应具有聚类性，或紧致性好，而不同类别样本应在特征空间中显示出具有较大的距离。统计模式识别各种方法实际上都是直接或间接以距离度量为基础的。常用的距离度量是D维特征空间中的欧氏距离 　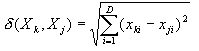　其中Xk,Xj表示两个样本的特征向量。xk、xj则是相应的第i个分量。 　　除此之外还有其它形式的距离度量，如 　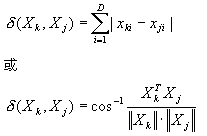　其中‖·‖表示向量的模，T表示向量转置符号。后续章节中还将提到另外一些距离度量的方式，它们都是为了度量相似性而设计的。 　　对事物进行分类本身是依据同类样本属性的相似性，在使用特征向量表示时，体现为同类样本在特征空间中靠的很近，因此可以用各种方法度量样本数据间的差异。一般说来，使用欧氏距离是最常用的，它表示两个向量的差向量的模，也就是本小节中第一个式子所计算的方法。这种计算在衡量几何距离时最为合适，例如各城市之间的距离。但在模式识别中特征向量的各个分量的含义往往是不同的，就像苹果的例子中，一个表示重量，一个表示直径，两者的单位都不一样，因此使用欧氏距离并不合理。一般来说样本的各个分量的分布范围在数量级上比较相近为好。 　　使用分量差的绝对值总和表示距离往往是对欧氏距离的简化，将平方计算改为了绝对值计算。课文中第三种方法主要反映两个特征向量的夹角，而没有反映特征向量幅值的差别。这些不同的相似度度量都有各自的优缺点，使用时要注意。 　　Java Applet演示 　　用户在矩形区域内点两个点，可以显示三种距离函数的数值。 　　1、(x1-x2)^2+(y1-y2)^2; 　　2、|x1-x2|+|y1-y2|; 　　3、夹角