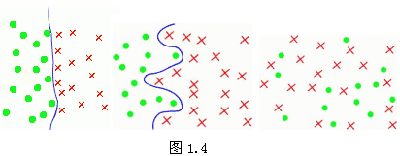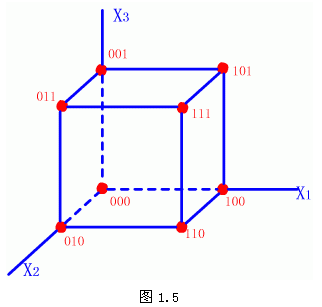
二、模式的紧致性 　　分类器设计难易程度与模式在特征空间的分布方式有密切关系，例如图1.4(a)、(b)与(c)分别表示了两类在空间分布的三种状况。其中(a)中两类样本存在各自明确的区域，它们之间的分界线(或面，超曲面)具有简单的形式，因而也较易区分，(b)中两类虽有各自不同的区域，但分界面的形式比较复杂，因而设计分类器的难度要大得多，如果遇到(c)类的情况则简直到了无法将它们正确分类的地步。 　　对于图1.4所表示的情况用什么概念来描述呢?这个概念称为模式的紧致性。为了说明这个概念，可以举图1.5例子来说明。图1.5中有一个立方体的8个端点，为8个样本。它们是由000，001，010，011，100，101，110，111八个点集组成。如果我们希望用平面将它们划分为A１与A２两类，显然这与它们的集合组成有关。例如如果A１由111，101，110，011组成，而A２由其余四个点组成，则只需要一个平面就可将它们分开。但若要分开A１={111,001,100,010}与Ａ２={000,011,101,110}这样两个集合，则需要三个平面。在这种情况下，A１集合中任一点的一位码变化，如111变成101，它就成为A２集合的成员。对A２也有如此情况。通常称处于两类的边界上的点为临界点，它们略一改变就会改变它们的类别，跨过边界去。那些非临界点则称为集合的内点，它们略有变化不会有类别变更的情况发生。拿这个定义来衡量，可以看出图1.4(a)只有少量的临界点，而(b)则是临界点的数量已经在总点数中占很高比例，其模式的紧致性就很差了。 　　根据以上讨论可以定义一个紧致集，它具有下列性质：(1)临界点的数量与总的点数相比很少。(2)集合中任意两个内点可以用光滑线连接，在该连线上的点也属于这个集合。(3)每个内点都有一个足够大的邻域，在该领域中只包含同一集合中的点。显然如果每个模式在特征空间的分布都满足上述要求的话，模式识别的问题在原则上就不会有什么困难。然而很多实际问题并不满足这个条件。许多问题在量测空间表示时往往不满足紧致性。但是如果它们的确是可分的话，这就意味着可以通过一种变换，使它们在相应的特征空间中界线分明，也就是具有了紧致性。模式识别系统设计的任务就是要寻找这样一种变换，即选择一种特征空间，使不同类别的样本能正确地分开。因此在我们讨论模式识别的问题时，通常假设同一类的各个模式在该空间中组成一个紧致集。至于如何找到这种变换还设有一种统一的有效的理论与方法。 　　对紧致性的理解不要拘泥于字面的定义，而可以从两个方面去理解。一是两类事物分布的区域不要有相互混迭的情况，就像国外一些国家不同种族的人混居区一样，仅用居住地点就无法判断是哪一个种类的人。另一种情况是事物尽管没有混居，但交界线很复杂，就像不同种族的居住区的边界像海岸线一样，犬牙交错，稍不留意，就会误入另一种族人的居住区。不要混迭，分界面干净利索就是一种形象的说法。 　　不同类数据分布的紧致与否，有的与数据本身有关，如手写体数字，同一数字的形态千差万别，就会使它们的特征向量也差异很大。不同种数字在特征空间的分布也就会相互混迭在一起，或界限不清。另一方面预处理也很重要，如印刷体数字，即使形态变异较小，但若在网格中的位置不固定，也会使特征向量表示出离散性，使紧致性变差。