一、学习 　　前面提到人们在日常生活中几乎时时刻刻在进行模式识别的活动，从小时候起就开始学习与增强这种能力。如小孩学习认字、认识事物都有一个从不会到会的过程。成人教小孩认字时，并不告诉“4”有什么特点，往往只是出示样本。孩子很快能总结出“4”的概念，不论该字是大还是小，形体笔划有多大变化，都能正确辨认出来。孩子的家长教孩子叫大人为爷爷、奶奶、伯伯、叔叔等，并没有告诉他们，什么样的人，具有什么特点的人应如何称呼，但孩子很快从所见到的爷爷的“样本”中学会该叫谁爷爷，很少有错误。孩子年龄很小时根本无法说明老年人有什么形体特征，也还不会描述事物，但却已经能够从学习过程中掌握了很强的分辨事物的能力。那么机器能做到这一点吗? 　　的确机器也有个学习过程，模式识别系统包括了训练这一环节与工作方式。但是在模式识别系统中，尤其是传统的模式识别技术中，信息获取，预处理，特征提取与选择一般都是设计者安排好的，机器本身无法从训练中培养出选择特征的能力，而训练的实质也只是按设计者拟订的数学公式，把训练样本提供的数据作为自变量执行计算求解的过程。一般说来人工神经元网络的学习能力比传统的模式识别方法要强。但目前看来，在人类尚无法了解自身的智力活动过程的现阶段，人类还不具备设计有高度智力的机器的能力。 　　确定分类决策的具体数学公式是通过分类器设计这个过程确定的。在模式识别学科中一般把这个过程称为训练与学习的过程。这是因为分类的规则是依据训练样本提供信息的确定的，在分类器的设计阶段。要使用一批训练样本，其中包括各种类别的样本，因此由这些样本可以大致勾画出各类事物在特征空间分布的规律性，从而为确定使用什么样的分类具体数学公式以及这些公式中的参数确定提供了信息。这种数学式子及其参数的确定应该说是综合设计者的人为因素以及训练样本提供的信息共同决定的。譬如在图1.3中两类训练样本的分布体现出近似圆形的分布。因此如能把这两个圆形区域确定下来，将它们的边界用某种数学式子近似，那么落在某一个圆形内的样本就可以用这种数学式子来判断。对于图1.3还可以看到，比较精确地表达不同类样本分布地聚集区不一定是必须的。用一条直线(线性方程)也许可以达到同样的目的。满足直线的方程是一个线性方程，写成f(x1,x2)=ax1+bx2+c=0，而不在该直线上的点则用f(x1,x2)是否大于零或小于零来分辨。使用直线的好处是计算方便，对一个实际分类问题，快速计算、快速分类是十分重要的。因此只要条件允许就要使用较简单的方法是一条基本原则。一般来说，决定使用什么类型的分类函数往往是人为决定的。但数学式子中的参数则往往通过学习来确定，这一点与人们学习新事物的方式很相似。人们常常从错误中吸取教训，纠正对事物不正确的认识。而分类器也有一种学习过程，如果发现当前采用的分类函数会造成分类错误，那么利用错误提供应如何纠正的信息，就可以使分类函数朝正确的方向前进，这就形成了一种迭代的过程，如果分类函数及其参数使出错的情况越来越少，就可以说是逐渐收敛，学习过程就收到了效果，设计也就可以结束。 　　本例子是为了演示分类决策函数。一种是按圆形区域划分两类点，用户如果在圆内点击，添加一个相同颜色的点，并显示到圆心的距离。另一种是线形分类器，按直线的上下分为两个区域，在一个区域内点击可以添加点。 　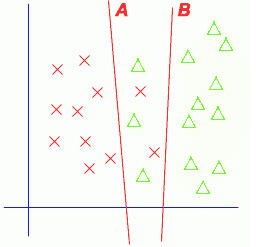　在后续章节的学习中我们会更加明确，所谓模式识别中的学习与训练是从训练样本提供的数据中找出某种数学式子的最优解，这个最优解使分类器得到一组参数，按这种参数设计的分类器使人们设计的某种准则达到极值。例如图1.3为两类别样本在二维特征空间中的分布。其中两类别样本分别用“×”与“△”表示。从图中可见这两类样本在二维特征空间中有相互穿插，也就是说这两类样本很难用简单的分界线将它们完全分开。如果我们用一直线作为分界线，称为线性分类器，对图中所示的样本分布情况，无论直线参数如何设计，总会有错分类发生。如果我们以错分类最小为原则分类，则图中A直线可能是最佳的分界线，它使错分类的样本数量为最小。但是如果将一个“×”样本错分成“△”类所造成的损失要比将“△”分成“×”类严重，则偏向使对“×”类样本的错分类进一步减少，可以使总的损失为最小，那末B直线就可能比A直线更适合作为分界线。可见分类器参数的选择或者学习过程得到的结果取决于设计者选择什么样的准则函数。不同准则函数的最优解对应不同的学习结果，得到性能不同的分类器。