定性是指特征的有与无,例如坦克与汽车都有驾驶装置,这不能作为区分它们的特征,但坦克有炮,汽车无炮,有没有炮是划分它们的一种有效特征。然而一些不同类别的事物往往具有相同的特征种类,或者用同样的特征度量去检测,但它们在这些特征的取值上有差别,在这种情况下特征值的取值范围成为辨别事物的重要依据。例如癌细胞与正常细胞都用同样的观察手段与量测手段去检测,而依据所得特征值分布范围将它们区分开来。在这种情况下,模式的特征集表示,又可写成处于同一个特征空间的特征向量表示。待识别的不同类模式都在同一特征空间中考察,不同类物体由于性质上的不同,它们在各特征取值范围上有所不同,因而在特征空间的不同区域中出现。本书就是在特征空间与特征向量这种表示模式的方法前提下,讨论模式识别的基本理论与基本方法。这种方法称为统计模式识别,是这门课的基本内容。
模式的描述方法:
对于具体事物的描述大体上可分为两种。一种是对事物的属性进行度量,属于定量的表示方法。另一种则是对事务所包含的成分进行分析,称为定性的描述或结构性描述。
定量的描述就是用各种尺度对事物进行度量。例如对水果进行分类,就需要对它的各种属性进行度量,水果的重量、大小、颜色、香味乃至味道等。由于对事物的度量是多方面的,因此要用合适的数据结构将它们记录下来,以便在同一种度量之间进行比较。常用的方法是将这些度量指排成序,譬如用水果的重量,近似球体直径。这两个指标按规定的先后排起来,如一只苹果重0.3斤,直径10厘米,则可表示成(0.3,1.0)。因此如看到一个数据为(0.35,12)则可解释成重量为0.35斤,直径12厘米。这种表示方法就称为向量表示法,该向量有两个分量,每个分量有自己特定的含义。
向量这个名字对某些人可能比较陌生。为了形象起见,我们可以用一个二维向量为例来说明,如一个二维向量A表示成(x,y),则(3,4)就是指x=3,y=4。如果用图像来表示,则可如图: |
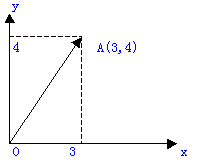 |
用式子表示,可写成: 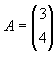 或A=(3,4)。 或A=(3,4)。
|
| 我们把前一种称为列向量,后一种称为行向量,在本课中主要用列向量表示,而将其相应的列向量表示叫做其“转置”,用符号T表示: |
如: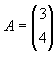 ,则
,则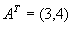 。
。 |
这时,有些同学可能会问,一个苹果的颜色用什么方式表示。这牵涉到颜色的表示方法。如果颜色只能用某些典型色来表示,如红、橙、蓝、绿、紫,那么,这种情况只能用代号表示,如令红为1号,橙为2号,等等。这样一来,上面提到的苹果如加上颜色描述,则可用一个三维向量,(0.35,10,1)t。对这些数字的理解要根据它的定义与所用单位来确定。对颜色的另一种表示方法,可以用常用的RGB表示。R,G,B分别表示三种基色成分,这本身就是一个三维向量,如与重量、尺度汇合在一起,就是一个五维的向量。
有一些事物用向量表示是不方便的,例如一幅景色图像中的房屋用向量描述就不一定方便,对房屋而言,它有屋顶、墙、门窗等组成,各种成分之间又有相互关系,则墙在屋顶之下,门与窗都在墙上等。这种由组成成分与相互关系表示的表示方法,最好用结构性的表示,常用的有串、树、图等。
在本门课中,我们主要使用向量表示方法。向量的每个元素称为特征,该向量也因此称为特征向量。
图像、像素的定义:
这里还要提出,在本门课中的举例与习题中常用图像作为例子,因此要说一下图像的表示方法。在计算机里分析的称为数字图像,它由排列整齐的二维网格组成,分为若干行与若干列,相当于一个二维数组,或称矩阵。我们称每个元素为像素,例如处在第三行第四列的元素的灰度值为155,则可表示成I(3,4)=155。
在本门课中都是对向量进行分析的,因此在概念上要把图像也表示成向量,譬如将图像像素一列一列串起来。实际上,只要记住向量的运算是建立在各个分量基础上的,例如:
|
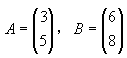 ,则 ,则
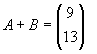
|
图像的运算也是按行列来进行,不要弄错行列。
此外,对于象语音信号这种随时间变化的信号,属于时域信号。此时,元素之间的时间先后顺序很重要,因此可用向量的形式将它们排列起来。说的严格一些,对语音信号进行采样,然后将在不同时刻采样值排列起来,组成向量。 |
|