（2）浮点数的尾数处理

　　在计算机中,浮点数的尾数总是用确定的位数来表示的,但浮点数的运算结果却常常超过给出的位数,如加减运算过程中的对阶和右规处理,会使尾数低位部分的一位或多位的值丢失；乘除运算也可有更多位数的结果。怎样处理多出来的这些位上的值,就是我们此处要讨论的问题。

　　第一种办法 是无条件地丢掉正常尾数最低位之后的全部数值。这种办法被称为截断处理,其好处是处理简单,问题是影响结果的精度。

　　第二种办法 运算过程中保留右移中移出的若干高位的值,最后再按某种规则用这些位上的值修正尾数。这种处理方法被称为舍入处理。

　　对原码表示的正、负数的尾数,舍入规则比较简单。最简便的方法,是只要尾数最低位为1,或移出的几位中有为1的数值位,就使最低位的值为1。另外一种办法是0舍1入法,即当丢失的最高位的值为1时,把这个1加到最低数值位上进行修正,否则舍去丢失的各位的值。这样处理时,舍入效果对正数负数是相同的,即入将使数的绝对值变大,舍则使数的绝对值变小。

　　但是,当尾数是用补码表示的时候,若丢失的位不是全零时,对正数来说,舍入规则与原码表示情况下的规则一致,对负数则正好相反,舍去丢掉位将使数的绝对值变大,入上丢掉位将使数的绝对值变小。从实用的角度考虑，此时所用的舍入规则,应该与用原码表示时产生相同的处理效果。具体规则是：
　　.当丢失的各位均为0时,不必舍入;
　　.当丢失的最高位为0,以下各位不全为0时,或者丢失的最高位为1,以下各位均为0时,则舍去丢失位上的值;
　　.当丢失的最高位为1,以下各位不全为0时,则执行在尾数最低位入1的修正操作。

　　看一些舍入处理的例子。
　　假定 [X]补 的值分别为101100000、101100001、101101000和101111001,在执行只保留小数点后四位有效数字的舍入操作后,其结果分别为10110(不舍不入情况),10110(舍)、10110(舍)和11000(入)。该执行结果,与变其为原码表示后再进行舍入,得到的是相同的真值,证明了上述对补码表示的负值给出的舍入规则是正确的。

　　下面我们给出浮点数相乘的一个实际的例子。假定浮点数的阶码为4位的移码,尾数(含符号位)为8位的原码,并规定不用隐含位,阶码的底为2,乘法的结果,尾数仍保留8位(含符号位),用尾数之后的四位值处理舍入操作,并直接用原码完成尾数的乘法运算。

　　假定 X = 2-5 * 0.1110011, Y = 23 * (-0.1110010)，则二数的浮点表示为:
　　[X]浮 = 0 011 0 1110011，[Y]浮 = 1 011 1 1110010

　　X*Y的执行步骤如下: 阶码为单符号位移码,尾数为单符号位原码。
　　乘积的阶码为二数阶码之和,用公式
　　[Ex + Ey]浮 = [Ex]浮 + [Ey]补
　　　0 011
　　+ 0 011
　
　　　0 110　　　　　为移码表示的-2

　　原码尾数相乘的结果为： 1 10101100110110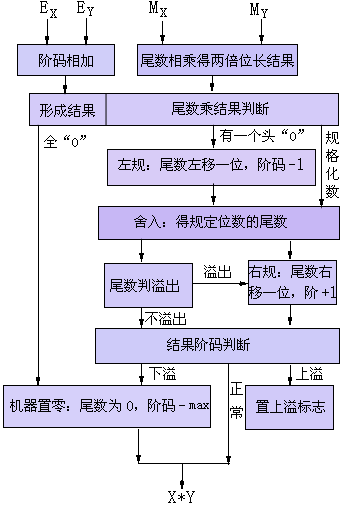
　　规格化处理，已满足规格化要求，不需左规,尾数不变,阶码仍为00110。
　　舍入处理，按舍入规则,尾数之后的四位为0110,可以直接"舍"掉。
　　所以相乘结果的最终值为 [X*Y]浮 = 0 110 1 1100110,其真值为2-2*(-0.1100110)

　　规格化浮点乘法运算流程如图2.22所示。


图2.22 规格化浮点乘法运算流程

　　执行浮点数乘法的运算步骤,也可用在浮点数除法的计算中,变乘为除,而且从舍入处理的要求看,还要多求几位商出来。