2. 浮点乘除法运算步骤
两个浮点数相乘,其乘积的阶码应为相乘的两个数的阶码之和,其尾数应为相乘二数的尾数之积。
两个浮点数相除,商的阶码应为被除数的阶码减去除数的阶码得到的差,尾数应为被除数的尾数除以除数的尾数所得的商。
乘除运算都可能出现结果溢出,或结果不满足规格化要求的问题,因此也必须进行这些检查和处理。与加减法运算类似的是,乘除法的浮点数运算也有个精度处理要求,舍入矛盾似乎更突出一点。下面就阶码运算和尾数舍入问题进行讨论。
(1)浮点数的阶码运算
对阶码的运算主要有 +1、-1、两阶码求和或两阶码求差四种,运算时还必须检查结果是否溢出。在计算机中,阶码通常用移码(或补码)形式表示。补码运算规则和判定溢出的方法,前一节已说明过了。这里只需对移码的运算规则和判定溢出的方法进行讲解。
移码的定义为
[X]移 = 2n + X -2n ≤X < 2n (Mod 2n+1)
按此定义,则有
[X]移 + [Y]移 = 2n + X + 2n + Y = 2n + (2n + X + Y)
= 2n + [ X + Y ]移
即直接用移码实现求阶码之和时,结果的最高位(符号位)多加了个1,要得到移码形式的结果,必须对结果的符号再执行一次求反操作。
考虑到对同一个数值,移码和补码的关系是,其数值位完全相同,而符号位正好相反。即[Y]补的定义为
[Y]补 = 2n+1 + Y
则很容易想到, 也可以用如下方式完成求阶码和的运算:
[X]移 + [Y]补 = 2n+ X + 2n+1 + Y
= 2n+1 + (2n + (X + Y)) (按2n+1 取模)
= [ X + Y ]移
同理有[X]移 + [-Y]补 = [ X - Y ]移。实际上这表明执行阶码加减运算时,对加数或减数送的是移码符号位正常该送的值的反码。
如果阶码运算的结果溢出,上述条件则不成立。此时,对使用双符号位的阶码加法器,规定移码的第二个符号位,即最高符号位恒用0参加加减运算,则溢出条件是最高符号位为1。此时,当低位符号位为0时,表明结果上溢,为1时,表明结果下溢。当最高符号位为0时,表明没有溢出,低位符号位为1,表明结果为正,为0时,表明结果为负。例如,假定阶码用四位表示,则其表示范围为-8到+7。看如下四种情况:
当 X = +011 , Y = +110 时,则有
[X]移 = 01 011, [Y]补 = 00 110, [-Y]补=11 010
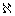 [
X + Y ]移 =[X]移 + [Y]补 = 10 001,
是结果上溢 [
X + Y ]移 =[X]移 + [Y]补 = 10 001,
是结果上溢
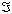 [
X - Y ]移 =[X]移 + [-Y]补 = 00 101,
结果正确,为-3 [
X - Y ]移 =[X]移 + [-Y]补 = 00 101,
结果正确,为-3
当 X = -011 , Y = -110时,则有
[X]移 = 00 101, [Y]补 = 11 010, [-Y]补=00
110
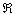 [
X + Y ]移 =[X]移 + [Y]补 = 11 111,
是结果下溢 [
X + Y ]移 =[X]移 + [Y]补 = 11 111,
是结果下溢
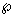 [
X - Y ]移 =[X]移 + [-Y]补 = 01 011,
结果正确,为-3 [
X - Y ]移 =[X]移 + [-Y]补 = 01 011,
结果正确,为-3
|