(2)补码两位乘
我们可以方便地从上一小节讲的、用比较法实现补码一位乘的方案,推导出补码两位乘的实现原理。当我们把补码两位乘理解为:合并原来两步补码一位乘为单步操作,则可找出如下对应关系。
假定上步乘法的部分积为 [Pi]补 ,本步的部分积应为
[Pi+1]补 =2-1 { [Pi]补 + ( Yn+1-i -Yn-i ) * [X]补 }
此后,下一步的部分积应为
[Pi+2]补 =2-1 { [Pi+1]补 + ( Yn-i -Yn-1-i ) * [X]补 }
将第一个公式中的 [Pi+1]补 代入第二个公式中时,则得到
[Pi+2]补 = 2-1 { 2-1
{ [Pi]补+( Yn+1-i -Yn-i
) *[X]补}+(Yn-i-Yn-1-i)*[X]补
}
= 2-2 { [Pi]补+ [ ( Yn+1-i
-Yn-i ) + 2 * ( Yn-i -Yn-1-i )
]*[X]补 }
= 2-2 { [Pi]补 + [ ( Yn+1-i
+Yn-i + 2 * Yn-1-i) ] * [X]补 }
(2.17)
公式(2.17)表明,在有了部分积 [Pi]补 之后,再求部分积 [Pi+2]补,
可用 [Pi]补 加上乘数寄存器最低两位与附加位三位值的组合结果与被乘数 [X]补
之积、再右移两位得到。
其中三位值的组合关系为
Yn+1-i + Yn-i + 2 * Yn-1-i
代入它们的八组取值,则得到
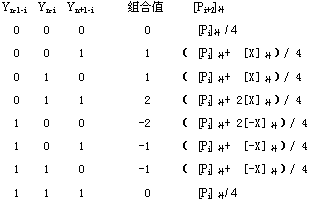
上表结果表明,执行补码两位乘的过程中,有部分积 +[X]补、部分积 +[-X]补、部分积
+2[X]补与部分积 +2[-X]补 四种操作。除需要有把 [X]补、[-X]补
送加法器的线路外,还需要有把[X]补、[-X]补左斜一位送加法器的线路。与此相应的,加法器应使用三位符号位,以避免
[X]左斜一位送加法器时运算结果溢出的情形。最后一点是,部分积和乘数每次应右移两位,运算器中应有支持右移两位的逻辑电路。
请注意:求部分积的次数和右移操作的控制问题。当乘数由1位符号和15位数据位组成时,求部分积的次数为 (1+15)/2 , 即8次
,而且最后一次的右移操作只右移一位。若数值位本身为偶数n,则必须再增加一位符号位,使总位数仍为偶数,此时求部分积的次数为n/2
+ 1,而且最后一次不再执行右移操作。
看一个两位补码乘的实例
假定 X = + 0.0110011 Y = - 0.0110010 [Y]=1 1001110
则 [X]补 = 0 0110011 [-X]补 = 1 1001101
2[X]补 = 0 1100110 2[-X]补 = 1 0011010
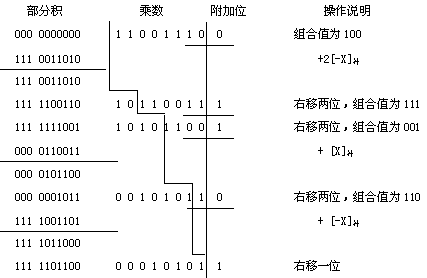
运算结果为 1 11011000001010,即为 -0.00100111110110
|

