下面是恢复余数除法的一个例子。 　　假定 X=0.1011 , Y=0.1101, 则有 [X]补 = 00 1011 　　　　　　　　 [Y]补 = 00 1101 , [-Y]补 = 11 0011 　　除法计算结束,二数符号异或为0,商是 +0.1101,余数为0.0111 * 2-4 ,余数0111是左移4次后得到的结果,所以真正的结果为这个值乘上2-4。若最后一次的余数为负,正确的余数应为 +Y 恢复后的正余数乘上2-4 。 　　这种方法的缺点是明显的，当某一次 -Ｙ的差值为负时，要多一次＋Y恢复正余数的操作,降低了执行速度,又使控制线路变得复杂,因此在计算机中很少采用。在计算机中普遍采用的是不恢复余数的除法方案,它是对恢复余数除法的一种修正措施,即当某一次减得的差值为负时,不是恢复它为正差值后再继续运算,而是设法直接用这个负的差值直接求下一位商,其实现原理叙述如下: 　　在恢复余数的除法运算中,若第i-1次求商时的余数为 +Ri-1 ,本次上商为1，下一次求商用的办法是 　　　　Ri= 2Ri-1 - Y 　　当Ri < 0时,第i位的商上0,而恢复余数的操作结果应为Ri + Y,下一次,即第i+1次求商的减法操作是 　　　　Ri+1= 2 (Ri+ Y ) - Y = 2 Ri + 2Y - Y = 2Ri+ Y 　　上述公式表明,当某一次求商,其减得的差值为负,即R<0时,本次上商为0,继续求下一位商时,可以不必恢复正余数,而是直接将负的差值左移一位(得2R)后,再采用加上除数的办法来完成,即通过判别2R+Y运算的结果为正还是为负。由此可得出不恢复余数的除法运算规则为: 　 　　当余数为正时,商上1,求下一位商的办法,是正余数左移一位,用减去除数的办法得到; 　　余数为负时,商上0,求下一位商的办法,是负余数左移一位,用加上除数的办法得到。即在本方案中,在求得本位商值的同时,还要影响到用减去还是用加上除数的操作继续求下一位商,所以不恢复余数除法又叫加减交替除法。 　　下面给出不恢复余数除法执行除运算过程的一个例子。用的还是X=0.1011,Y=0.1101这两个值, [X]补 = 00 1011 , [Y]补 = 00 1101 , [-Y]补 = 11 0011。 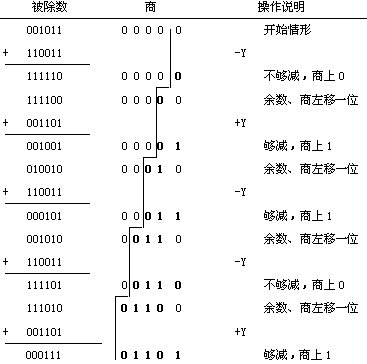　　运算结果,商的数值位为1101,符号位为相除二数符号的异或值0,结果为+0.1101。 原码一位除的不恢复余数的运算过程的详细控制流程如图2.9所示。 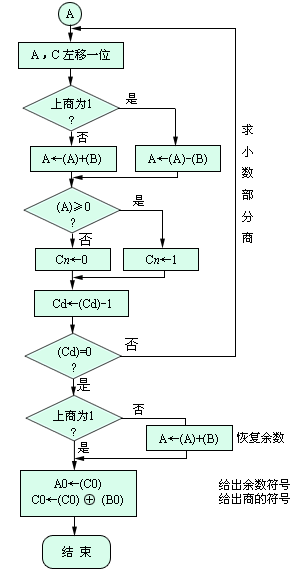图2.9 不恢复余数除法的运算的控制过程 　　至此,我们可把定点原码一位除的实现方案小结如下: 　　(1) 对定点小数除法,首先要比较除数和被除数的绝对值的大小,需要防止出现数值溢出的错误。 　　(2) 商的符号为相除二数的符号的半加和。 　　(3) 计算机中用加减交替法实现除法运算时,被除数的位数可以是除数的两倍,其低位的数值部分，开始时放在用于保存商的寄存器中。运算过程中,放被除数和商的寄存器同时左移一位。 　　(4) 在计算机中,求差和移位是在同一个操作步骤中完成的,而不是像我们书面写的那种形式用两个步骤完成。