|
(3) 反码表示法,是用机器数的最高一位代表符号,数值位是对负数值各位取反的表示方法,其定义为
[X]反 = 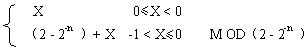 (2.14) (2.14)
例如, X=+0.1011, [X]反 =01011
X=-0.1011, [X]反 =10100
正数的反码与其原码、补码相同。
反码的性质:
① 在反码表示中,机器数最高位为符号位,0代表正号,1代表负号,负数的机器数和它的真值之间的关系为:
[X]反 = ((2-2-n)+X) MOD(2-2-n)
用反码进行两数相加时,若最高位有进位,还必须把该进位值加到结果的最低位,才能得到真正的结果,这一操作通称 "循环进位"。
X= +0.1011, Y=-0.0100,有[X]反 =01011, [Y]反 =11011,
[X+Y]反 = [X]反 + [Y]反 = 01011 + 11011 = 100110,最高位有进位,要加到结果的最低位,得
00110 + 00001 = 00111,即 +0.0111。
又如, X= +0.1011, Y= +0.0100,[X+Y]反 = [X]反 + [Y]反 = 01011+00100=01111,最高位无进位值,得到的已是最终结果。
② 在反码表示中,零有两个编码,即
[+0.0]反 = 00000 , [-0.0]反 = 11111
有人也称反码为1的补码(One's Complement),它的实际模为2-2-n。这里的-n为最低位的位序号。
用反码实现算术运算不方便,0值又有两个编码,用得不很普遍。
|