为了介绍派生数据类型,首先介绍一种通用的数据类型描述方法--类型图。使用类型图可以用比较精确和形式化的方法来描述各种各样的类型。类型图是一系列二元组的集合,两个数据类型是否相同取决于它们的类型图是否相同。类型图的二元组为如下形式:
| 图13-1 类型图的图示 <基类型,偏移> |
| 则类型图为 类型图={<基类型0,偏移0>,<基类型1,偏移1>,...,<基类型n-1,偏移n-1>} |
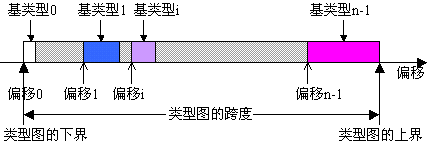 |
基类型指出了该类型图中包括哪些基本的数据类型,而偏移则指出该基类型在整个类型图中的起始位置。基类型可以是预定义类型或派生类型,偏移可正可负,没有递增或递减的顺序要求。而一个类型图中包括的所有基类型的集合称为某类型的类型表,表示为:
类型表={基类型0,...,基类型n-1}
将类型图和一个数据缓冲区的基地址结合起来,可以说明一个通信缓冲区内的数据分布情况。
预定义数据类型是通用数据类型的特例,比如MPI_INT是一个预先定义好了的数据类型句柄,其类型图为{(int, 0)},有一个基类型入口项int和偏移0。其它的基本数据类型与此相似。数据类型的跨度被定义为该数据类型的类型图中从第一个基类型到最后一个基类型间的距离。
即如果某一个类型的类型图为
typemap={(type0,disp0),...,(typen-1,dispn-1)},
则该类型图的下界定义为
lb(typemap)=min {dispj}, 0=<j<=n-1
则该类型图的上界定义为
ub(typemap)=max(dispj+sizeof(typej)), 0=<j<=n-1
该类型图的跨度定义为:
extent(typemap)=ub(typemap)-lb(typemap)+e
由于不同的类型有不同的对齐位置的要求,e就是能够使类型图的跨度满足该类型的类型表中的所有的类型都能达到下一个对齐要求所需要的最小非负整数值。
假设type={(double,0),(char,8)}(一个double型的值在偏移0,后面在偏移8处跟一个字符值)。进一步假设double型的值必须严格分配到地址为8的倍数的存储空间。则该数据类型的extent是16(从9循环到下一个8的倍数)。一个由一个字符或面紧跟一个双精度值的数据类型,其extent也是16。
复制数据类型
MPI_TYPE_CONTIGUOUS(count,oldtype,newtype)
IN count 复制个数(非负整数)
IN oldtype 旧数据类型(句柄)
OUT newtype 新数据类型(句柄)
int MPI_Type_contiguous(int count,MPI_Datatype oldtype, MPI_Datatype *newtype)
MPI_TYPE_CONTIGUOUS(COUNT,OLDTYPE,NEWTYPE,IERROR)
INTEGER COUNT,OLDTYPE,NEWTYPE,IERROR
用MPI_TYPE_CONTIGUOUS构造新的数据类型,设原来的数据类型oldtype的类型图为
{(doubel,0),(char,8)},其中类型的跨度为extent=16,对旧类型重复的次数count=3,则newtype返回的新类型的类型图为
{(double,0),(char,8),(double,16),(char,24),(double,32),(char,40)}
| 图13-2 用MPI_TYPE_CONTIGUOUS产生的新类型 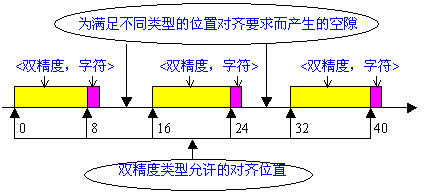 |