 定义11.4.2
对实数集R,<是R上的小于关系, 定义11.4.2
对实数集R,<是R上的小于关系,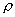 是R上的距离函数,若 是R上的距离函数,若 , ,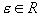 且 且 ,则集合 ,则集合
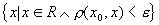
称为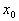 的 的 邻域。 邻域。
 定义11.4.3
对实数集R, 定义11.4.3
对实数集R,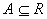 , ,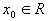 ,如果在 ,如果在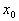 的任一个 的任一个 邻域中,都存在不等于 邻域中,都存在不等于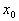 的元素x,且 的元素x,且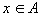 ,则称 ,则称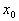 是A的一个极限点(或凝聚点)。 是A的一个极限点(或凝聚点)。
定义的条件可以写成
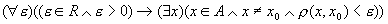
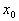 是A的极限点意味着,A中的元素可以无限接近 是A的极限点意味着,A中的元素可以无限接近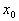 ,即存在一个A的不含有 ,即存在一个A的不含有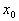 的子集,可以排列成极限为 的子集,可以排列成极限为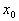 的序列。直观地说,在 的序列。直观地说,在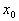 附近,A的点是稠密的。 附近,A的点是稠密的。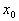 不一定在A中。 不一定在A中。
 例1
对 例1
对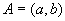 ,其中 ,其中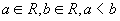 ,开区间A中的元素和 ,开区间A中的元素和 都是A的极限点,即A的极限点的集合是 都是A的极限点,即A的极限点的集合是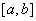 。 。
对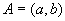 ,其中 ,其中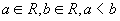 ,闭区间A的极限点的集合是A。 ,闭区间A的极限点的集合是A。
 例2
对 例2
对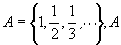 的极限点是0。 的极限点是0。
空集没有极限点。有限集合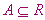 没有极限点。有理数集Q的极限点集合是实数集R,因为在任一实数附近,有理数和无理数都是稠密的。 没有极限点。有理数集Q的极限点集合是实数集R,因为在任一实数附近,有理数和无理数都是稠密的。
 定理11.4.1
对实数集R, 定理11.4.1
对实数集R,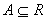 , ,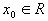 , ,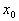 是A的极限点当且仅当在A中存在点列 是A的极限点当且仅当在A中存在点列
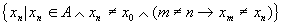
使得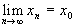 。
。
 定理11.4.2
若 定理11.4.2
若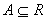 是有界无限集,则A具有极限点。 是有界无限集,则A具有极限点。
 例3
设 例3
设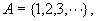 则A没有极限点。 则A没有极限点。
 定义11.4.4
对实数集R, 定义11.4.4
对实数集R,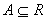 , ,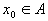 ,若 ,若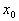 不是A的极限点,则称 不是A的极限点,则称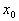 为A的孤立点。 为A的孤立点。
A的极限点可以在A中,也可不在A中。A的孤立点一定在A中。A中的点,或为A的极限点,或为A的孤立点。
 定义11.4.5
对实数集R, 定义11.4.5
对实数集R,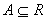 ,A的所有极限点的集合称为A的导集,记作A'。如果 ,A的所有极限点的集合称为A的导集,记作A'。如果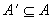 ,则称A为闭集。 ,则称A为闭集。
对于闭集A,导集A'是A的子集,即A的极限点都在A中。
另外具有以下性质:
A的闭包为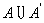 ; ;
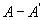 中的点叫A的孤立点; 中的点叫A的孤立点;
当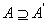 时,A叫闭的; 时,A叫闭的;
当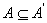 时,A叫自密的; 时,A叫自密的;
当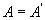 时,A叫完全的,换句话说,没有孤立点的闭集叫完全集。 时,A叫完全的,换句话说,没有孤立点的闭集叫完全集。
导集具有以下性质:
(3) 因为空集没有极限点,所以有
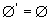 ; ;
(4) 对任一点p, 是空的,所以有 是空的,所以有
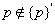
(5) 若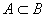 ,则显然有 ,则显然有
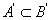
(6) 若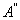 表示A的导集的导集,令 表示A的导集的导集,令 ,那么 ,那么
 所有开集, 所有开集,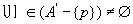 ,因此有一点 ,因此有一点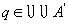 ,
,
由于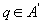 , ,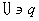 ,所以 ,所以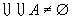 , , ,
,
因而有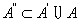 。
。
(5)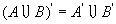 。
。
 例4
对 例4
对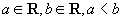 则 则
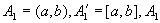 不是闭集。 不是闭集。
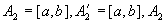 是闭集。 是闭集。
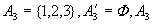 是闭集。 是闭集。
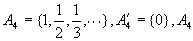 不是闭集。 不是闭集。
因为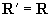 ,所以 ,所以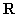 是闭集。因为 是闭集。因为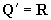 ,所以有理数集 ,所以有理数集 不是闭集。因为 不是闭集。因为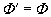 ,所以 ,所以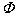 是闭集。 是闭集。
 定理11.4.3
对实数集R, 定理11.4.3
对实数集R,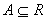 ,则A'是闭集,即 ,则A'是闭集,即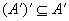 。 。
 定理11.4.4
任意个闭集的交集是闭集。有限个闭集的并集是闭集。 定理11.4.4
任意个闭集的交集是闭集。有限个闭集的并集是闭集。
若一族闭集合 ,它们的交为F, ,它们的交为F,
设x不属于F,则
x至少不属于 中的某一集合,譬如 中的某一集合,譬如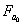 ,因为 ,因为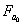 为闭集,故有 为闭集,故有 ,使 ,使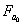
中没有一点和x点的距离小于 。 。
显然F中没有一点和x点的距离小于 。 。
因而F为一闭集。
 例5
设 例5
设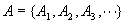 ,其中 ,其中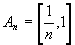 都是闭集。但是 都是闭集。但是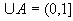 不是闭集。由此可见,无限个闭集的并集不一定是闭集。 不是闭集。由此可见,无限个闭集的并集不一定是闭集。
|