 定义10.8.7
对偏序集 定义10.8.7
对偏序集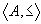 ,对任意的 ,对任意的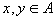 ,若 ,若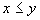 或 或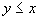 ,则称x和y是可比的。 ,则称x和y是可比的。
 定义10.8.8
对偏序集 定义10.8.8
对偏序集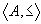 ,如果对任意的 ,如果对任意的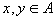 ,x和y都可比,则称≤为A上的全序关系,或称线序关系。并称 ,x和y都可比,则称≤为A上的全序关系,或称线序关系。并称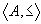 为全序集。 为全序集。
全序集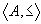 就是对任意 就是对任意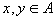 ,或者有 ,或者有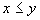 或者有 或者有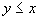 成立。 成立。
 例9
N上的小于等于关系是全序关系,所以 例9
N上的小于等于关系是全序关系,所以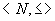 是全序集。 是全序集。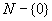 上的整除关系不是全序关系。对非空集合 上的整除关系不是全序关系。对非空集合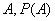 上的包含关系不是全序关系。 上的包含关系不是全序关系。
 定义10.8.9
对偏序集 定义10.8.9
对偏序集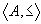 ,且 ,且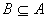 ,进一步 ,进一步
(1)如果对任意的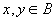 ,x和y都是可比的,则称B为A上的链,B中元素个数称为链的长度。 ,x和y都是可比的,则称B为A上的链,B中元素个数称为链的长度。
(2)如果对任意的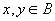 ,x和y都不是可比的,则称B为A上的反链,B中元素个数称为反链的长度。 ,x和y都不是可比的,则称B为A上的反链,B中元素个数称为反链的长度。
 例10
对例8中的偏序集。{2,4,12},{3,6,18},{3,9},{18}都是链。{4,6,9},{12,18},{4,9}都是反链。 例10
对例8中的偏序集。{2,4,12},{3,6,18},{3,9},{18}都是链。{4,6,9},{12,18},{4,9}都是反链。
对全序集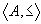 ,显然A是链。A的任何子集都是链。 ,显然A是链。A的任何子集都是链。
 定理10.8.4
对偏序集 定理10.8.4
对偏序集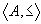 ,设A中最长链的长度是n,则将A中元素分成不相交的反链,反链个数至少是n。 ,设A中最长链的长度是n,则将A中元素分成不相交的反链,反链个数至少是n。
 证明
施归纳于n。 证明
施归纳于n。
当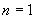 时,A本身就是一条反链,定理结论成立。(这时≤是恒等关系) 时,A本身就是一条反链,定理结论成立。(这时≤是恒等关系)
假设对于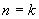 ,结论成立。考虑 ,结论成立。考虑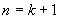 的情况。当A中最长链的长度为 的情况。当A中最长链的长度为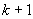 时,令M为A中极大元的集合,显然M是一条反链。而且 时,令M为A中极大元的集合,显然M是一条反链。而且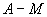 中最长链的长度为k。由归纳假设,可以把 中最长链的长度为k。由归纳假设,可以把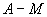 分成至少k个不相交的反链,加上反链M,则A可分成至少 分成至少k个不相交的反链,加上反链M,则A可分成至少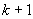 条反链。 条反链。
这个定理称为偏序集的分解定理,这是组合学三大存在性定理之一,有广泛的应用。
 定理10.8.5
对偏序集 定理10.8.5
对偏序集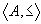 ,若A中元素为 ,若A中元素为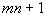 ,则A中或者存在一条长度为 ,则A中或者存在一条长度为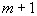 的反链,或者存在一条长度为 的反链,或者存在一条长度为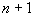 的链。 的链。
|