 定义10.8.5
对偏序集 定义10.8.5
对偏序集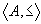 ,且 ,且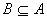 ,进一步 ,进一步
(1) 若 ,则称y为B的最小元, ,则称y为B的最小元,
(2) 若 ,则称y为B的最大元, ,则称y为B的最大元,
(3) 若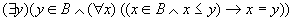 ,则称y为B的极小元, ,则称y为B的极小元,
(4) 若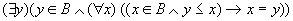 ,则称y为B的极大元。 ,则称y为B的极大元。
 例7
在例4的偏序集 例7
在例4的偏序集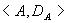 的哈斯图中.令 的哈斯图中.令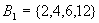 ,则 ,则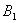 的最大元和极大元是12,最小元和极小元是2。令 的最大元和极大元是12,最小元和极小元是2。令 ,则 ,则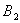 的极大元是4和6,极小元是2和3,有最大元和最小元。 的极大元是4和6,极小元是2和3,有最大元和最小元。
注意区别最小元与极小元。B的最小元应小于等于B中其他各元。B的极小元应不大于B中其他各元(它小于等于B中一些元,并与B中另一些元无关系)。B的最大元(最小元),一定是B的极大元(极小元)。最小元(最大元)不一定存在,若存在必唯一。在非空有限集合B中,极小元(极大元)必存在,不一定唯一。
从上述定义可以知道,当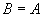 时,则偏序集 时,则偏序集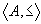 的极大元即是哈斯图中最顶层的元素,其极小元是哈斯图中最底层的元素,不同的极小元素或不同的极大元素之间是无关的。 的极大元即是哈斯图中最顶层的元素,其极小元是哈斯图中最底层的元素,不同的极小元素或不同的极大元素之间是无关的。
 定义10.8.6
对偏序集 定义10.8.6
对偏序集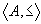 ,且 ,且 ,进一步 ,进一步
(1) 若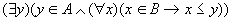 ,则称y为B的上界, ,则称y为B的上界,
(2) 若 ,则称y为B的下界, ,则称y为B的下界,
(3) 若集合 ,则C的最小元称为B的上确界或最小上界, ,则C的最小元称为B的上确界或最小上界,
(4) 若集合 ,则C的最大元称为B的下确界或最大下界。 ,则C的最大元称为B的下确界或最大下界。
 例8
集合 例8
集合 上的整除关系 上的整除关系 偏序关系。偏序集 偏序关系。偏序集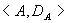 的哈斯图如图10.8.3所示。 的哈斯图如图10.8.3所示。
 图
10.8.3 图
10.8.3
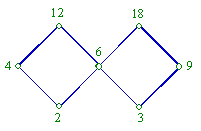
 的上界是4和12,上确界是4,下界和下确界是2。 的上界是4和12,上确界是4,下界和下确界是2。 没有上下界,没有上下确界。 没有上下界,没有上下确界。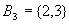 的上界是6,12,18,上确界是6,没有下界和下确界。 的上界是6,12,18,上确界是6,没有下界和下确界。
B的上下界和上下确界可能在B中,可能不在B中,但一定在A中。上界(下界)不一定存在,不一定唯一。上确界(下确界)不一定存在,若存在必唯一。
|
