 定理10.5.4
对非空集合A上的关系R,有 定理10.5.4
对非空集合A上的关系R,有
(1)R是自反的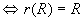 , ,
(2)R是对称的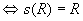 , ,
(3)R是传递的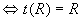 。 。
 证明 证明
(1)先设R是自反的。因为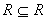 ,且任何包含R的自反关系 ,且任何包含R的自反关系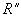 ,有 ,有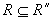 。所以,R满足 。所以,R满足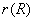 的定义, 的定义,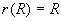 。
。
再设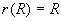 。由 。由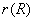 的定义,R是自反的。 的定义,R是自反的。
(2)和(3)的证明类似。
 定理10.5.5
对非空集合A上的关系 定理10.5.5
对非空集合A上的关系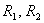 ,若 ,若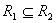 ,则 ,则
(1)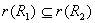 , ,
(2)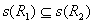 , ,
(3)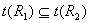 。 。
证明留作思考题。
 定理10.5.6
对非空集合A上的关系 定理10.5.6
对非空集合A上的关系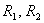 ,则 ,则
(1)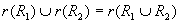 , ,
(2)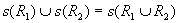 , ,
(3)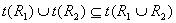 。 。
 证明 证明
(1)因为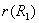 和 和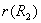 都是A上自反的关系,所以 都是A上自反的关系,所以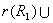 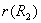 是A上自反的关系。由 是A上自反的关系。由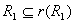 和 和 ,有 ,有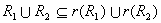 。所以
。所以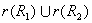 是包含 是包含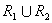 的自反关系。由自反闭包定义,
的自反关系。由自反闭包定义,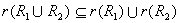 。 。
因为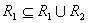 ,有 ,有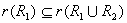 。类似地 。类似地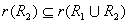 。则 。则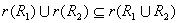 。 。
(2)和(3)的证明留作思考题。
注意,定理的结论(3)是包含关系,不是相等关系。下面是真包含的例子。
 例4
集合 例4
集合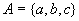 上的关系 上的关系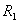 和 和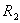 为, 为,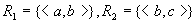 。于是, 。于是,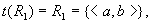 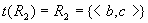 。则有
。则有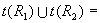 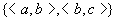 。但是
。但是 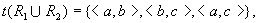 显然 显然
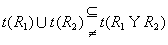
|