子集公理模式是
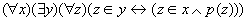
子集公理模式是说,对任意的集合x,存在x的子集x,x的元素x使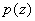 为真。它主要用于下列情况。一直若干满足条件 为真。它主要用于下列情况。一直若干满足条件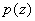 的元素,但不知这些元素能否组成一个集合。这是只要找到一个集合A,使这些满足条件的元素都有 的元素,但不知这些元素能否组成一个集合。这是只要找到一个集合A,使这些满足条件的元素都有 。这样就可以由A和 。这样就可以由A和 用分离公理得到集合 用分离公理得到集合
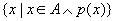
这就是那些元素组成的集合。
下面用子集公理模式证明交集、差集、广义交和笛卡儿积的存在性。
 定理9.7.1
对任意的集合A和B,交集 定理9.7.1
对任意的集合A和B,交集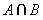 是集合。 是集合。
 证明
对集合A,选取 证明
对集合A,选取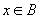 为子集公理模式中的 为子集公理模式中的 ,由子集公理存在集合 ,由子集公理存在集合
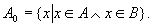
所以, 是集合。 是集合。
 定理9.7.2
对任意的集合A和B,差集A-B是集合。 定理9.7.2
对任意的集合A和B,差集A-B是集合。
 证明
由集合和谓词公式 证明
由集合和谓词公式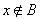 , 依据子集公理, 存在集合
, 依据子集公理, 存在集合

所以,  是集合。 是集合。
 定理9.7.3
对任意的非空集合A,广义交 定理9.7.3
对任意的非空集合A,广义交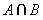 是集合。 是集合。
 证明
对非空集A,存在 证明
对非空集A,存在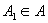 , , 选取公式)为 选取公式)为 。依据子集公理,对集合 。依据子集公理,对集合 和上述公式,存在集合 和上述公式,存在集合
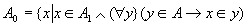
此外  . .
由 和 和 可以推出 可以推出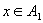 ,所以 ,所以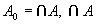 是集合。 是集合。
 定理9.7.4
对任意的集合A和B,
笛卡儿积A×B是集合。 定理9.7.4
对任意的集合A和B,
笛卡儿积A×B是集合。
 证明
对任意的 证明
对任意的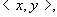 有
有
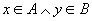

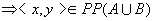 (定理9.5.18) (定理9.5.18)
显然 是集合,
选取公式 是集合,
选取公式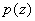 为 为
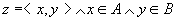
可以构造它的子集
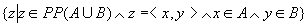
这就是A×B,所以A×B是集合。
下面是一个重要结论,它可用子集公理来证明:
 定理9.7.5
不存在集合A,使任一集合都是A的元素。 定理9.7.5
不存在集合A,使任一集合都是A的元素。
 证明
假设存在集合A,
任一集合是A的元素,
选 证明
假设存在集合A,
任一集合是A的元素,
选 为 为 , 依据子集公理, 存在集合
, 依据子集公理, 存在集合
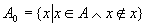 , ,
即  . .
取 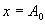 ,则有 ,则有
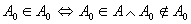 . .
如果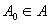 ,就有
,就有 ,这是不可能的。所以
,这是不可能的。所以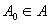 ,与假设矛盾,定理得证。 ,与假设矛盾,定理得证。
下面说明,为什么以前规定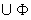 不存在? 不存在?
假设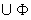 是集合,则由广义交的定义, 是集合,则由广义交的定义,
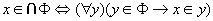 . .
因为 永假, 所以右式永真。于是左式
永假, 所以右式永真。于是左式 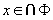 对所有x永真。于是 对所有x永真。于是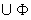 是所有集合的集合,与定理9.7.5矛盾。因此规定 是所有集合的集合,与定理9.7.5矛盾。因此规定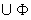 不存在。 不存在。
|