 (1)外延公理
两个集合相等的充要条件是它们恰好具有同样的元素。 (1)外延公理
两个集合相等的充要条件是它们恰好具有同样的元素。
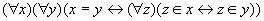
 (2)空集合存在公理
存在不含任何元素的集合(空集 (2)空集合存在公理
存在不含任何元素的集合(空集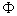 )。 )。
 x是空集 x是空集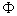
这个公理定义了集合论中第一个集合,空集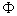 。由外延公理可知,空集是唯一的。 。由外延公理可知,空集是唯一的。
 (3)无序对集合存在公理
对任意的集合x和y,存在一个集合z,它的元素恰好为x和y (3)无序对集合存在公理
对任意的集合x和y,存在一个集合z,它的元素恰好为x和y

在x=y时,
这个公理构造出恰好一个元素的集合,如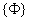 和 和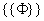 。在x≠y时,这个公理构造出两个元素的集合,如 。在x≠y时,这个公理构造出两个元素的集合,如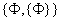 和 和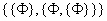 。 。
 (4)并集合公理
对任意的集合x,存在一个集合y,它的元素恰好为x的元素的元素。 (4)并集合公理
对任意的集合x,存在一个集合y,它的元素恰好为x的元素的元素。

这个公理可以由集合{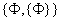 , ,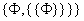 构造集合 构造集合 , ,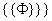 。它解决了广义并存在性(集合的广义并是集合)。由无序对集合存在公理和并集合公理,可以解决两个集合并集的存在性(并集是集合)。 。它解决了广义并存在性(集合的广义并是集合)。由无序对集合存在公理和并集合公理,可以解决两个集合并集的存在性(并集是集合)。
 (5)子集公理模式(分离公理模式)
对于任意的谓词公式 (5)子集公理模式(分离公理模式)
对于任意的谓词公式 ,对任意的集合x,存在一个集合y,它的元素z恰好既是x的元素又使 ,对任意的集合x,存在一个集合y,它的元素z恰好既是x的元素又使 为真。 为真。

对一个具体的谓词(谓词常项) ,子集公理模式就是一条公理。对不同的 ,子集公理模式就是一条公理。对不同的 ,它是不同的公理。所以,子集公理模式不是一条公理,而是无限多条有同样模式的公理。因此称为公理模式。在9.7.2节将介绍用子集公理模式解决交集、差集、广义交和笛卡儿积的存在性(集合经这些运算得到的都是集合)。 ,它是不同的公理。所以,子集公理模式不是一条公理,而是无限多条有同样模式的公理。因此称为公理模式。在9.7.2节将介绍用子集公理模式解决交集、差集、广义交和笛卡儿积的存在性(集合经这些运算得到的都是集合)。
 (6)幂集公理
对任意的集合x,
存在一个集合y,它的元素恰好是x的子集。 (6)幂集公理
对任意的集合x,
存在一个集合y,它的元素恰好是x的子集。
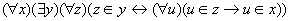
公理指出幂集的存在性(集合的幂集是集合)。
 (7)正则公理
对任意的非空集合x,存在x的一个元素,它和x不相交。 (7)正则公理
对任意的非空集合x,存在x的一个元素,它和x不相交。
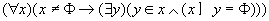
正则公理将在9.7.3中说明, 它排除了奇异集合, 防止发生悖论。
 (8)无穷公理
存在一个由所有自然数组成的集合。 (8)无穷公理
存在一个由所有自然数组成的集合。
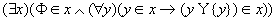
式中的x是自然数集合N。在9.7.4中将说明自然数的定义和无穷公理。这个公理构造了第一个无限集合。
|