笛卡儿积具有下列基本性质。
(1)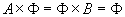 ,
,
(2)若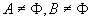 且 且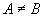 ,
则 ,
则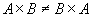 ,
,
(3)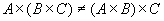 .
.
结果表明, 笛卡儿积不满足交换律和结合律, 结论(3)是因为
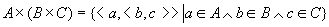
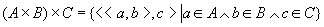
其中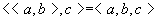 是三元组,
但 是三元组,
但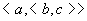 不是三元组。 不是三元组。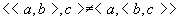 .
.
 定理9.5.18
若A是集合, 定理9.5.18
若A是集合,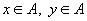 ,则 ,则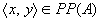 。 。 。 。
 证明 证明
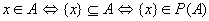 ,且 ,且
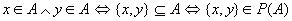 . .
由以上二式可得到
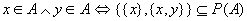
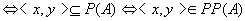 . .
 定理9.5.19
对任意的集合A,B和C, 定理9.5.19
对任意的集合A,B和C,
(1)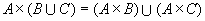
(2)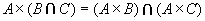
(3)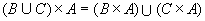
(4)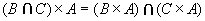
 证明
只证(1), 其余留作思考题。 证明
只证(1), 其余留作思考题。
对任意的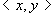 ,可得 ,可得
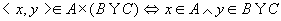
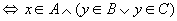
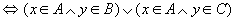
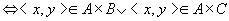
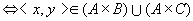
所以,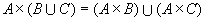 。
。
 定理9.5.20
对任意的集合A,B和C,若 定理9.5.20
对任意的集合A,B和C,若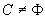 ,则
,则
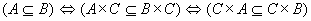
 证明
先设 证明
先设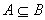 ,若 ,若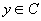 ,则 ,则
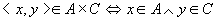
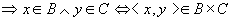
所以, 。
。
再设 。取 。取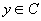 ,则 ,则
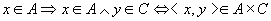
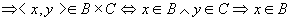 . .
所以,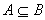 。
。
总之,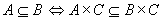 。 。
类似可证,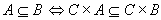 。
。
 定理9.5.21
对任意的集合A,B,C和D, 定理9.5.21
对任意的集合A,B,C和D,
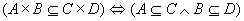
 证明
先设 证明
先设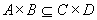 ,对任意的 ,对任意的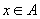 ,因存在 ,因存在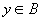 ,则 ,则
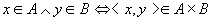
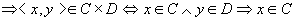
所以,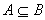 ,类似有 ,类似有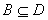 。 。
再设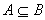 且 且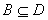 。对任意的x,y有 。对任意的x,y有
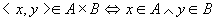
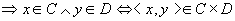
所以,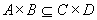 。
。
|