下面讨论广义并和广义交对于传递集合的封闭性。
 定理9.5.14
若集合A是传递集合,则YA是传递集合。 定理9.5.14
若集合A是传递集合,则YA是传递集合。
 证明
对任意的x和y,有 证明
对任意的x和y,有
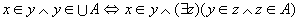
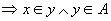 (A是传递集合) (A是传递集合)

所以UA是传递集合。
 定理9.5.15
若集合A的元素都是传递集合,则UA是传递集合。 定理9.5.15
若集合A的元素都是传递集合,则UA是传递集合。
 证明
对任意的x和y,有 证明
对任意的x和y,有
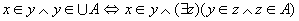
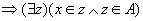 (Z是传递集合) (Z是传递集合)

所以UA是传递集合。
 定理9.5.16
若非空集合A是传递集合,则 定理9.5.16
若非空集合A是传递集合,则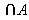 是传递集合,且 是传递集合,且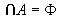 。
。
这个定理的证明要使用正则公理, 这里不给出证明。
 定理9.5.17
若非空集合A的元素都是传递集合,则 定理9.5.17
若非空集合A的元素都是传递集合,则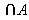 是传递集合。 是传递集合。
 证明
对任意的x和y,可得 证明
对任意的x和y,可得
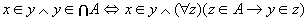
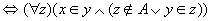
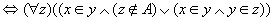
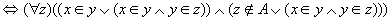
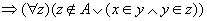
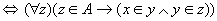
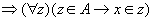 (Z是传递集合) (Z是传递集合)

所以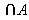 是传递集合。 是传递集合。
|