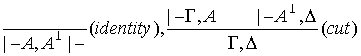
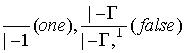
a.恒等式及否定规则 　　 　　b.结构规则 　　（Γ'是Γ的任一置换） 　　c.逻辑规则 　　 　　， 　　 (no rule for zero) 　　(left plus) 　　(right plus) 　　(of course), (weakening) 　　(dereliction), (contraction) 　　(for all:x is not free in Г), 　　 (there is) 　　语法说明 　　（1） 线性逻辑有四个常项 1, ┴; T, 0 。逻辑联结词是，￡ (乘法联结词)，AB 是公式 A┴ ￡ B 的简写。，& (加法联结词)。对原子公式 p,q,r… 等等，它们的线性否定是事先给定的 p┴,q┴,r┴,… 但若 A 是一个复杂公式，A┴ 仅只是简写，比如(AB)┴ 只是 A┴￡B┴ 的简写。而并不是因为该两公式在线性逻辑系统中是逻辑等价的。归纳简写方法见上一节的 关于，￡，，& 的De Morgan 等式。 　　（2） !，？是模态联结词。 ！-- of course, ? --- why not 。 　　（3） 以上罗列的推理规则中，去掉带模态联结词 ! , ? 的规则，余下的部分则构成线性谓词串形演算。如果再去掉带量词, , 再余下的部分就是线性命题串形演算。这是线性逻辑的核心部分。经典的命题演算中含有如此结构优美的一个子逻辑系统，是令人惊讶的。