在程序流图中，我们称具有下列性质的结点序列为一个循环： 　　① 它们是强连通的。也即，其中任意两个结点之间，必有一条通路，而且该通路上各结点都属于该结点序列。如果序列只包含一个结点，则必有一有向边从该结点引到其自身。 　　② 它们中间有且只有一个是入口结点。所谓入口结点，是指序列中具有下述性质的结点： 　　从序列外某结点，有一有向边引到它，或者它就是程序流图的首结点。 　　因此，我们定义的循环就是程序流图中具有唯一入口结点的强连通子图，从循环外要进入循环，必须首先经过循环的入口结点。 图 11.12程序流图 　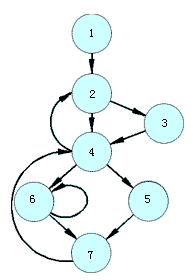　例如，图11.12中的程序流图，根据定义，结点序列｛6｝，｛4，5，6，7｝以及｛2，3，4，5，6，7｝都是循环；而结点序列｛2，4｝，｛2，3，4｝，｛4，6，7｝以及｛4，5，7｝虽然都是强连通的，但因它们的入口结点不唯一，所以都不是上述意义下的循环。 不难看出,图11.11中的程序流图里,｛B2，B3｝是程序中的循环，而B2是唯一的入口结点。