当一个文法中相同左部非终结符的右部存在能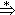  ε的情况则必须知道该非终结符的后跟符号的集合中是否含有其它右部开始符号集合的元素。 ε的情况则必须知道该非终结符的后跟符号的集合中是否含有其它右部开始符号集合的元素。
为此,我们定义一个文法非终结符的后跟符号的集合如下:
 定义5.2 设 G=(VT,VN,S,P)是上下文无关
文法,A∈VN,S是开始符号
定义5.2 设 G=(VT,VN,S,P)是上下文无关
文法,A∈VN,S是开始符号
FOLLOW(A)={a|S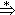  μAβ,且a∈VT,a∈FIRST(β),μ∈VT*
,β∈V+} μAβ,且a∈VT,a∈FIRST(β),μ∈VT*
,β∈V+}
若S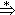  μAβ,且β μAβ,且β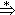  ε,
则#∈FOLLOW(A)。 ε,
则#∈FOLLOW(A)。
也可定义为:FOLLOW(A)={a|S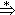  …Aa…,a ∈VT}
…Aa…,a ∈VT}
若有S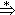  …A,则规定#∈FOLLOW(A)
…A,则规定#∈FOLLOW(A)
这里我们用'#'作为输入串的结束符,或称为句子括号,如:#输入串#。
因此当文法中含有形如:
A→α
A→β
的产生式时,其中A∈VN,α,β∈V*,当α,β不同时推导出空时,设α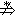 ε,β ε,β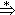  ε,则当FIRST(α)∩(
FIRST(β)∪FOLLOW(A))= ε,则当FIRST(α)∩(
FIRST(β)∪FOLLOW(A))=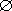  时,对于非终结符A的替换仍可唯一地确定候选。 时,对于非终结符A的替换仍可唯一地确定候选。
综合以上情况可定义选择集合SELECT如下:
 定义5.3 给定上下文无关文法的产生式A→α, A∈VN,α∈V*,
若α
定义5.3 给定上下文无关文法的产生式A→α, A∈VN,α∈V*,
若α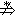 ε,则SELECT(A→α)=FIRST(α) ε,则SELECT(A→α)=FIRST(α)
如果α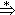  ε,则SELECT(A→α)=FIRST(α\ε)∪FOLLOW(A)。 ε,则SELECT(A→α)=FIRST(α\ε)∪FOLLOW(A)。
FIRST(α\ε)表示FIRST(α)的非{ε}元素。
更进一步可以看出能够使用自顶向下分析技术必须使文法满足如下条件,我们称满足条件的文法为LL(1)文法,其定义为:
 定义5.4 一个上下文无关文法是LL(1)文法的充分必要条件是:对每个非终结符A的两个不同产生式,A→α, A→β,满足
定义5.4 一个上下文无关文法是LL(1)文法的充分必要条件是:对每个非终结符A的两个不同产生式,A→α, A→β,满足
SELECT(A→α)∩SELECT(A→β)=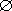 
其中α,β不同时能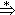  ε ε |