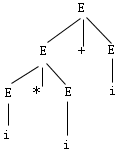
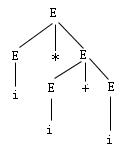
图4.4 推导一的语法树 图4.5 推导二的语法树 　　例4.11的文法G是二义的。 　　注意：文法的二义性和语言的二义性是两个不同的概念。因为可能有两个不同的文法G和G′，其中G是二义的，但是却有L(G)=L(G′)，也就是说，这两个文法所产生的语言是相同的。如果产生上下文无关语言的每一个文法都是二义的，则说此语言是先天二义的。对于一个程序设计语言来说，常常希望它的文法是无二义的，因为希望对它的每个语句的分析是唯一的。 　　人们已经证明，要判定任给的一个上下文无关文法是否为二义的，或它是否产生一个先天二义的上下文无关语言，这两个问题是递归不可解的。即，不存在一个算法，它能在有限步骤内，确切判定任给的一个文法是否为二义的。我们所能做的事是为无二义性寻找一组充分条件(当然它们未必都是必要的)。例如，在例4.11的文法中，假若规定了运算符'+'与'*'的优先顺序和结合规则，即按惯例，让'*'的优先性高于'+'，且它们都服从左结合，那么就可以构造出一个无二义文法，如例4.14的文法。 例4.14   　　定义表达式的无二义文法G[E]： 　　E→T|E+T 　　T→F|T*F 　　F→(E)|i 　　它和例4.11的文法产生的语言是相同的。即它们是等价的。