我们所介绍的方法称为"语法制导"的方法,即按正规式的语法结构指引构造过程,首先将正规式分解成一系列子表达式,然后使用如下规则为R构造NFA,对R的各种语法结构的构造规则具体描述如下:
①(a)对于正规式
 |
 |
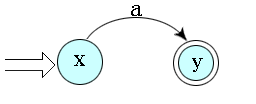 |
(a) 对正规式R=s|t,所构造的NFA(R)如下:
 |
(b) 对正规式R=st,所构造的NFA(R)为:
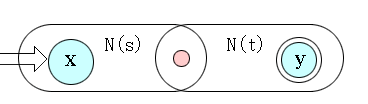 |
| 下面介绍从Σ上的一个正规式R构造Σ上的一个NFA M,使得L(M)=L(R)的方法。 我们所介绍的方法称为"语法制导"的方法,即按正规式的语法结构指引构造过程,首先将正规式分解成一系列子表达式,然后使用如下规则为R构造NFA,对R的各种语法结构的构造规则具体描述如下: ①(a)对于正规式
(a) 对正规式R=s|t,所构造的NFA(R)如下:
(b) 对正规式R=st,所构造的NFA(R)为:
|