① 对∏每一个状态组G进行下述工作:
将G划分为子组。G的两个状态s和t分在同一子组的充要条件是:对所有的输入符号a,状态s和t的a转换都是∏的同一组中的状态。
②形成的所有子组成为∏new的状态组。
| 图4.8 DFA M和DFA M' |
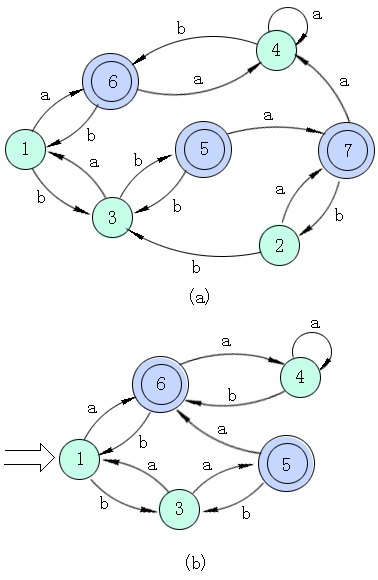 |
首先将M的状态分成两个子集:一个由终态(可接受态)组成,一个由非终态组成,这个初始划分P0为:P0=({1,2,3,4},{5,6,7}),显然第一个子集中的任何状态都与第二个子集中的任何状态不等价。
现在观察第一个子集{1,2,3,4},在读入输入符号a后,状态3和4分别转换为第一个子集中所含的状态1和4,而1和2分别转换为第二个子集中所含的状态6和7,这就意味着{1,2}中的状态和{3,4}中的任何状态在读入a后到达了不等价的状态,因此{1,2}中的任何状态与{3,4}中的任何状态都是可区别的,因此得到了新的划分P1如下:
P1=({1,2}{3,4}{5,6,7})
下面试图在P1中寻找一个子集和一个输入符号使得这个子集中的状态可区别,P1中的子集{3,4}对应输入符号a将再分割,而得到划分P2=({1,2},{3},{4},{5,6,7})。
P2中的{5,6,7}可由输入符号a或b而分割,得到划分P3=({1,2},{3},{4},{5},{6,7})。
经过考察,P3不能再划分了。令1代表{1,2}消去2,令6代表{6,7},消去7,我们便得到了图4.8(b)的DFA M′,它是4.8(a)的DFA M的最小化。
比起原来的有穷自动机,化简了的有穷自动机具有较少的状态,因而在计算机上实现起来将简洁些。