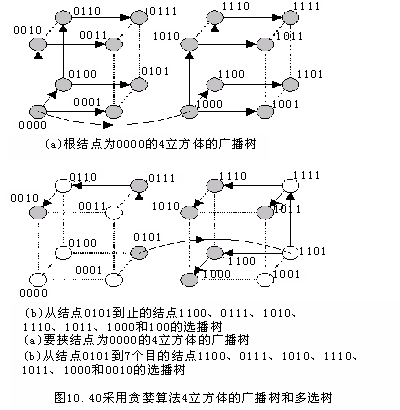
为在n方体上实现广播，可用类似的生成树，时延不超过n就能到达所有结点。图10.40a是一个根结点为0000的4立方体。超立方体广播树的流量最小。
图10.40b是一棵贪婪选播树，可从结点0101发送包到7个目的结点。这个贪婪选播算法的基本思想是向那些可达到最多剩余目的结点的维方向发送包。
从源结点S＝0101开始，由维2方向可以到达2个目的结点，由维4方向可以达到5个目的结点。因此，第一层所用的通道是0101
0111和01011101。从结点1101，由维2方向可以到达3个目的结点，由维1方向可以到达4个目的结点。因此，第二层所用的通道是1101
1111，11011100和01110110。同理，第三层所用的通道是1111
1110，11111011，11001000和01100010。第四层所用的通道是11101010。在扩充选播树时，首先应该比较所有各维方向的可达性(reachability)，然后选择某些维使剩余目的结点的集合最小。如果两维之间有连线，那么选择其中任何一维都可以。因此，所生成的树不是唯一的。
已经证明贪婪选播算法所需的通道数与多次单播或广播树相比要少。在虫蚀寻径网络中，实现选播操作时，每个结点的寻径器应有复制片缓冲区中数据的能力。
为了与选播树或广播树的增长同步，树中同一层的所有输出通道必须在传输向前推进一层之前处于就绪状态，否则中间结点需要增加缓冲区。
