4. 均匀洗牌置换
　　均匀洗牌置换是将输入端分成数目相等的两半，前一半和后一半按序一个隔一个地从头至尾依次与输出端相连。这好比洗扑克牌时，将整副牌分成相等的两叠来洗。达到理想的一张隔一张的均匀情况。故称为均匀洗牌置换，或简称为洗牌置换。其函数关系可表示为：
　　由此表达式可见，洗牌变换是将输入端二进制地址循环左移一位即得到对应的输出端二进制址。
　　逆均匀洗牌是均匀洗牌的逆函数，二者所完成的变换图形的输入端和输出端正好互换了个位置，其函数表达式为：
　　逆洗牌是将输入端二进制地址编号循环右移一位即得到相应的输出端地址。
　　均匀洗牌与逆均匀洗牌是两种十分有用的互连函数，以它们代表的链路与以交换置换代表的开关多级组合起来可构成网络与逆网络。s函数在实现多项式求值、矩阵转置和FFT等并行运算以及并行排序等方面都得到广泛的应用。

　　5. 蝶式置换
　　蝶式置换的名称由来于FFT变换的实现时其图形的形状如蝴蝶式样。这里，它被定义为：
　　这种置换是将输入端二进地址的最高位和最低位互换位置即可求得相应输出端的地址。

　　6.位序颠倒置换
　　位序颠倒置换是将输入端二进制地址的位序颠倒过来求得相应输出的地址。其表达式为：
　　在实现FFT时，最后一步要将结果整序，也就是将结果按二进制位序颠倒重新排列，以获得最后的变换值。

　　7. 移数置换
　　移数置换是将输入端数组循环移动一定的位置向输出端传输。其函数表示式无需用二进制编号来写，可表达如下：
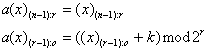
　　k为常数，指移过的位置值，也可以将整个输入数组分成若干个子数组，在子数组内进行循环移数置换，这种段内循环移数的表达式可写成为两个式子如下：
　　其中下标(n-1):r和(r-1):o分别指从n-1位到r位和从r-1位到o位。
　　循环移数置换的变换图形见图10.27。

　　这种置换在实现并行计算和图象处理中都很有用。
图10.27 N＝8移数置换