有限差分方法是求解场方程的一种有效方法。它把一个有规则的网格履盖在整个场域上，用网格点上变量值写出差分方程组以代替场方程来进行计算。在解决物理问题时，如果将描述平面场的拉普拉依方程：
中的二阶偏导数表示为差分形式： 
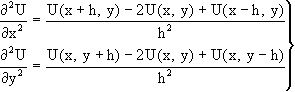
并代入原方程，则可得有限
差分计算公式：
式中，(x, y)为平面直角坐标，h为网格间距。
Illiac IV的阵列结构特别适用于计算这种在网格上定义的有限差分函数。根据有限差分计算公式，任一网格点(x, y)上的函数值可由其四周邻近点的函数值计算出来，这一要求正好反映了阵列处理机每一处理单元与其四个近邻连接的性质。实际计算时，应利用张弛法进行。每一网格点上的函数值用求其四邻平均值的方法计算，经多次迭代，逐次逼近其最终的平均值。网格边缘的函数值是已知的，由场域的边界条件决定；而对于内部各点的函数值，开始时可选择为零，然后根据式有限差分计算公式多次迭代求U(x, y)值，直至连续二次迭代所求值的差小于规定误差为止(已知迭代过程是收敛的)。
IlliacIV在计算时，是把内部网格点分配给各个处理单元的。因此，上述计算过程可以并行地完成，从而可几十倍地提高处理速度。由于实际问题中所遇到的内部网格点数目往往是很大的，因此需要将其分成许多子网格，然后才能在Illiac IV上求解。