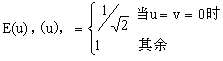离散余弦变换，在数字图像数据压缩编码技术中，可与最佳变换K-L变换媲美，因为DCT与K-L变换压缩性能和误差很接近，而DCT计算复杂度适中，又具有可分离特性，还有快速算法等特点，所以近年来在图像数据压缩中，采用离散余弦变换编码的方案很多，特别是90年代迅速崛起的计算机多媒体技术中，JPEG、MPEG、H.261等压缩标准，都用到离散余弦变换编码进行数据压缩。
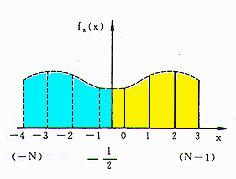
4.20 偶对称
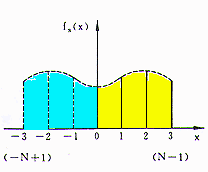
4.21 奇对称
1. 一维离散余弦变换
设一维离散函数f(x)，x=0，1，…，N-1，把f(x)扩展成为偶函数的方法有两种，以N=4为例，可得出如图4.20和图4.21所示的两种情况。图4.20称偶对称，图4.21称奇对称，从而有偶离散余弦变换（EDCT）和奇离散余弦变换（ODCT）。
由图4.20和4.21看出，对于偶对称扩展，对称轴在
处。
（4.43）采样点数增到2N。
奇对称扩展，对称轴在x=0处。
（4.44）采样点数增到2N－1。
由离散傅里叶变换定义出发，对公式（4.43）作傅里叶变换，以
表示，则得
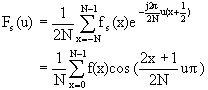（4.45） 式中，
当
当
当
，
，且，
考虑正变换公式与逆变换公式的对称性，令
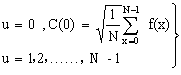（4.46）
（4.47）式中
（4.48）
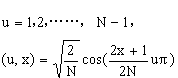（4.49）定义式（4.46）和式（4.47）为离散偶余弦正变换公式；式（4.48）和式（4.49）为离散偶余弦变换核公式。
离散偶余弦逆变换公式为
（4.50）x = 0，1，…，N-1
将公式（4.46）和公式（4.47）合并、化简，可得到一维离散偶余弦正变换公式，即
（4.51）式中
当
时，
当
时，
2. 二维离散偶余弦变换
设 空域变量取值范围为
频域变量取值范围为
，那么，二维离散偶余弦正变换公式为
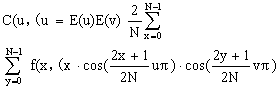（4.52）式中u = 0，1，…，N-1
v = 0，1，…，N-1
当
，
当
，
二维离散偶余弦逆变换公式
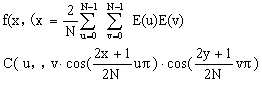（4.53）式中
当
当
，
二维离散余弦变换核具有可分离特性，所以，其正变换和逆变换均可将二维变换分解成一系列一维变换（行、列）进行计算。
3. 借助FFT实现离散余弦变换
由公式(4.46)和公式(4.47)一维离散偶余弦正变换公式，略加变换，即
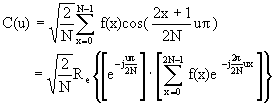（4.54）式中，
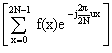可用FFT算法计算，其结果乘以
，取实部即可得到离散余弦变换结果。计算FFT时，x=0，1，…，2N-1求和，但实际上，在x=N，N+1，…，2N+1范围内，f(x)均得零，故仍然计算N个点。4. 二维快速离散余弦变换
二维快速离散余弦变换算法，是直接对二维图像数据
逐层对半分块，并重新排列数据，直至被分割的子块尺寸为1×1为止。这种算法既不是将二维分离成行、列，再进行一系列的一维变换算法，也不是借助于FFT，再取实部的算法。二维快速余弦变换，只需做实数乘法和加法，对于x方向取样点数为M，y方向采样点数为N的f(x，y)图像数据块，其快速余弦变换的实数乘法次数为
。为了公式推导简化，把采样点数MN和常数4都放在正变换式中。即正变换（DCT）
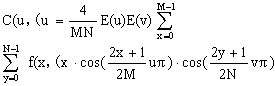（4.55）式中u= 0，1，…，M-1
v= 0，1，…，N-1
其中，
逆变换(IDCT)
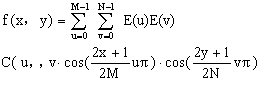（4.56）式中
其中，
