
利用预测编码可以去除图像数据的时间和空间的冗余,直观、简捷和容易实现,特别适用于硬件实现,对于传输速率高的地方,大多用此法。但是预测编码的压缩能力有限,DPCM一般压缩到2~4bit/s。变换编码是进行一种函数变换,不是直接对空域图像信号编码,而是首先将空域图像信号映射变换到另一个正交矢量空间(变换域、或频域),产生一批变换系数,然后对这些变换系数进行编码处理。
1.变换编码原理
变换编码是进行一种函数变换,不是直接对空域图像信号编码,而是首先将空域图像信号映射变换到另一个正交矢量空间(变换域、或频域),产生一批变换系数,然后对这些变换系数进行编码处理。

变换编码的理论基础是"联合信息熵必不大于各分量信息熵之和。"也就是说,对于联合信源(x,y),其冗余度也隐含在信源间的相关性之中,通常不易直接对各分量进行编码;应尽量去除各分量间的相关性。
现在举一个例子,设有两个相邻的数据样本x1与x2,每样本采用3bit编码,因此各有23=8个幅度等级。而两个样本的联合事件,共有8×8=64种可能性,可用图4.5-1的二维平面坐标表示。其中x1轴与x2轴分别表示相邻两样本可能的幅度等级。对于慢变信号,相邻两样本x1与x2同时出现相近幅度等级的可能性较大。因此,如图4.5-1(a)阴影区内45。斜线附近的联合事件,其出现概率也就较大,不妨将此阴影区之边界称为相关圈。信源的相关性愈强,则相关圈愈加扁长。或者形象地说,x1与x2呈现"水涨船高"的紧密关联特性。为了要对圈内各点的位置进行编码,就要对两个差不多大的坐标值分别进行编码。当相关性愈弱时,此相关圈就愈显方圆形状,说明x1处于某一幅度等级时,x2可能出现在不相同的任意幅度等级上。
例如:
·两个相邻的数据样本x1与x2
·每样本采用3bit编码,各有23=8个幅度等级
·两个样本的联合事件,共有8×8=64种可能性
·用图4.5-1的二维平面坐标表示。
4.5-1 正交变换的几何意义

(a)子图像在阴影区中的概率大小
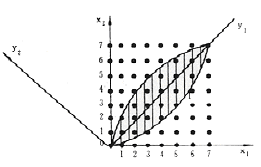
(b)坐标系旋转后的情况

现在若对该数据对进行正交变换,从几何上相当于坐标系旋转45。,变成y1,y2坐标系,如图4.5-1(b)所示。那么此时该相关圈正好处在y1坐标轴上下,且该圈愈扁长,其在y1上的投影就愈大,而在y2上的投影就愈小。因而从y1,y2坐标来看,任凭y1在较大范围内变化,而y2却巍然"不动"或"只有微动"。这就意味着变量y1和y2之间在统计更加相互独立。因此,通过这种坐标系旋转变换,就能得到一组去掉大部分甚至全部统计相关性的另一种输出样本。
变换编码技术已有近30年的历史,技术上比较成熟,理论也比较完备,广泛应用于各种图像数据压缩,诸如单色图像、彩色图像、静止图像、运动图像,以及多媒体计算机技术中的电视帧内图像压缩和帧间图像压缩等。
正交变换的种类很多,如傅立叶(Fouries)变换、沃尔什(Walsh)变换、哈尔(Haar)变换、斜(slant)变换、余弦变换、正弦变换、K-L(Karhunen - Loeve)变换等。
|

