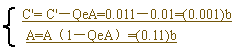与霍夫曼编码不同, 算术编码(Arithmetic Coding)跳出了分组编码的范畴,从全序列出发,采用递推形式的连续编码。它不是将单个的信源符号映射成一个码字,而是将整个输入符号序列映射为实数轴上[0,1]区间内的一个小区间,其长度等于该序列的概率;再在该小区间内选择一个代表性的二进制小数,作为实际的编码输出,从而达到了高效编码的目的。不论是否二元信源,也不论数据的概率分布如何,其平均码长均能逼近信源的熵。
算术编码方法比霍夫曼编码等熵编码方法要复杂,但是它不需要传送像霍夫曼编码的霍夫曼码表,同时算术编码还有自适应能力的优点,所以算术编码是实现高效压缩数据中很有前途的编码方法。这也是我们学习算术编码的意义。
下面讲第一个问题:算术编码基本原理
1.算术编码基本原理
算术编码方法是将被编码的信息表示成实数0和1之间的一个间隔。信息越长编码表示它的间隙就越小,表示这一间隙所须二进位就越多,大概率符号出现的概率越大对应于区间愈宽,可用长度较短的码字表示;小概率符号出现概率越小层间愈窄,需要较长码字表示。
信息源中连续的符号根据某一模式生成概率的大小来减少间隔。可能出现的符号要比不太可能出现的符号减少范围少,因此只增加了较少的比特位。

这样说完可能大家对算术编码的原理还不大理解,那我们来将以下算术编码的实现原理。
2.算术编码实现步骤
设数据序列有两种符号组成,其概率各不相同(一大一小),称概率大的为大概率符号,以MPS(Most Probable Symbol)表示大概率符号,其概率用Pe代表;称概率小的为小概率符号,用LPS(Least
Probable Symbol)表示小概率符号,其概率用Qe代表;
3.算术编码算法的实现

下面我们介绍子区间起始位置(头)和子区间宽的计算方法,并通过例子说明其过程。
设置两个专用寄存器,A寄存器和C寄存器,

设C寄存器内的数值为子区间的起始位置,A寄存器内的数值为子区间的宽度,初始化时C=0,A=1。
初始化时:C=0,表示子区间[0,1]的起始点
A=1。表示子区间的宽度
当低概率符号LPS到来时
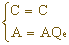
当高概率符号MPS到来时
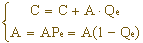

C+A等于子区间的右端点,算术编码的结果落在子区间内。输入编码符号串中大概率的符号出现频率愈高,对应的子区间变宽,这时可用短的码字表示编码结果;相反输入符号串中小概率的符号出现频率增加,相应的子区间变窄,落入该区间的编码结果,需要一个长的码字表示。下面我们举一个简单的例子,加以具体说明编码过程。
对一个"1011"符号串进行算术编码。
4.解码算法及举例

解码是编码的逆过程。在解码过程中同样设置两个寄存器C'和寄存器A。C'寄存器和A寄存器中的内容,要根据每次符号"1"--MPS或"0"--LPS按照以下公式修改。
C'是已知的算术编码还原成小数的值,例如上面的算术数编码结果是"011"那么C'=0.011,A是区间长度,初始值为"1"。
C'是已知的算术编码还原成小数的值,A=1
当C'落在0~QeA子区间内,解码符号赋以"0"-LPS,
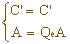
当C'落在QeA~A子区间内,解码符号赋以"1"--MPS,
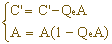

利用上述公式多次重复计算,求得与解码输入符号串所对应的解码输出。解码结果是由"0"、"1"构成的符号串。现在以上面编码结果"011"为例,对它进行解码。
例题:已知算术编码结果为"011",对其解码,求原信源序列符号。
解:由编码过程可知,"1"为大概率符号,"0"为小概率符号;
大概率Pe=3/4,小概率Qe=1/4;
C'=0.011;A=1
(1)QeA=1/4=(0.01)b
C'=(0.011)b 落在QeA~A(0.01~1)子区间,解码符号赋以MPS--"1"
"1"就是解码所得的第一个符号。
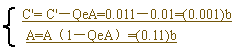
(2)QeA=0.01×0.11=(0.0010110)b
C'=0.001 落在0~QeA(0~0.0010110)子区间,解码符号赋LPS以"0"
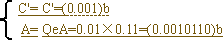
(3)QeA=0.01×0.0011=(0.000011)b
C'=0.001 落在QeA~A(0.000011~1)子区间,解码符号赋以MPS——“1”
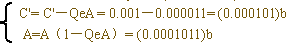
(4)QeA=0.01×0.11101=(0.00001)b
C'=(0.000101)b 落在QeA~A(0.00001~1)子区间,解码符号赋以MPS——“1”
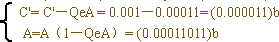

以上进行4次分割,计算的结果是“1011”,与原编码完全相同。
解码为:1011

以上我们讨论的都是假设大概率符号“MPS”恒定为“1”,小概率符号“LPS”恒定为“0”,而实际上应该随着它们在被编码符号串中出现的概率而自适应地改变。也就是说随着输入符号的变化,自动修改Qe和Pe的值。一说算术编码具有自适应的能力。
当信源概率比较接近时,建议使用算术编码,因为此时霍夫曼编码的结果趋于定长码,效率不高。根据T.Bell等人对主要的统计编码方法的比较,算术编码具有最高的压缩效率。
但实现上,算术编码比霍夫曼编码复杂,特别是硬件。
算术编码也是变长编码,因此,算术编码也使用于分段信息。在误差扩散方面,比分组码要严重,因为它是从全序列出发来编码的,一旦有误码,就会一直延续下去。因而算术编码的传输要求高质量的信道,或采用检错反馈重发的方式。
值得指出的是,实际上并不存在某种唯一的“算术码”,而是有一大类算术编码的方法。仅IBM公司便拥有数十项关于算术编码的专利。
|