
数据压缩的理论基础是信息论。也就是说经典的数据压缩技术是建立在信息论的基础之上的。数据压缩的理论极限是信息熵。
认真学习本书的"第三章理论极限与基本途径"
数据压缩的理论基础是信息论,数据压缩的理论极限是信息熵。

那么,我们首先要明确信息熵的概念,这个概念很重要,它是学习数据压缩编码技术的一个最基本的概念,如果这个概念搞不清楚的化,就等于没有一点数据压缩技术的理论基础,不仅影响统计编码的学习,而且也将影响其他编码技术的学习。所以信息熵的这个概念一定要掌握!在讲信息熵之前要有两个基本概念的铺垫,这两个基本概念就是信息、信息量。首先第一个概念"信息"。
1.信息
信息是用不确定的量度定义的,
是用不确定性的量度定义的,
也就是说信息被假设为由一系列的随机变量所代表,它们往往用随机出现的符号来表示。我们称输出这些符号的源为"信源"。也就是要进行研究与压缩的对象。
被假设为由一系列的随机变量所代表,它们往往用随机出现的符号来表示。

要注意理解这个概念中的"不确定性"、"随机"性、"度量"性,也就是说当你收到一条消息(一定内容)之前,某一事件处于不确定的状态中,当你收到消息后,分解除不确定性,从而获得信息,因此去除不确定性的多少就成为信息的度量。
比如:你在考试过后,没收到考试成绩(考试成绩通知为消息)之前,你不知道你的考试成绩是否及格,那么你就处于一个不确定的状态;当你收到成绩通知(消息)是
"及格",此时,你就去除了"不及格"(不确定状态,占50%),你得到了消息--"及格"。
一个消息的可能性愈小,其信息含量愈大;反之,消息的可能性愈大,其信息含量愈小。
第二个概念是信息量。
2.信息量

指从N个相等的可能事件中选出一个事件所需要的信息度量和含量。也可以说是辨别N个事件中特定事件所需提问"是"或"否"的最小次数。
(1)指从N个相等的可能事件中选出一个事件所需要的信息度量和含量。辨别N个事件中特定事件所需提问"是"或"否"的最小次数。

例如:从64个数(1~64的整数)中选定某一个数(采用折半查找算法),提问:"是否大于32?",则不论回答是与否,都消去半数的可能事件,如此下去,只要问6次这类问题,就可以从64个数中选定一个数,则所需的信息量是
=6(bit)
例如:从64个数(1~64的整数)中选定某一个数
则所需的信息量是 =6(bit)

我们现在可以换一种方式定义信息量,也就是信息论中信息量的定义。
设从N中选定任一个数X的概率为P(x),假定任选一个数的概率都相等,即P(x)=1/N,则信息量I (x)可定义为: 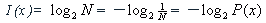
设从N中选定任一个数X的概率为P(x),假定任选一个数的概率都相等,即P(x)=1/N,则信息量I
(x)可定义为: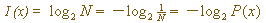

上式可随对数所用"底"的不同而取不同的值,因而其单位也就不同。设底取大于1的整数α,考虑一般物理器件的二态性,通常α取2,相应的信息量单位为比特(bit);当α=e,相应的信息量单位为奈特(Nat);当α=10,相应的信息量单位为哈特(Hart);
设底取大于1的整数α,
α=2,相应的信息量单位为比特(bit);
当α=e,相应的信息量单位为奈特(Nat);
当α=10,相应的信息量单位为哈特(Hart);

显然,当随机事件x发生的先验概率P(x)大时,算出的I(x)小,那么这个事件发生的可能性大,不确定性小,事件一旦发生后提供的信息量也少。必然事件的P(x)等于1,
I(x)等于0,所以必然事件的消息报导,不含任何信息量;但是一件人们都没有估计到的事件(P(x)极小),一旦发生后,I(x)大,包含的信息量很大。所以随机事件的先验概率,与事件发生后所产生的信息量,有密切关系。I(x)称x发生后的自信息量,它也是一个随机变量。
P(x)大时,算出的I(x)小 必然事件的P(x)等于1, I(x)等于0。
P(x)小时,算出的I(x)大 必然事件的P(x)等于0, I(x)等于1。
I(x)称x发生后的自信息量,它也是一个随机变量。

现在可以给"熵"下个定义了。信息量计算的是一个信源的某一个事件(X)的自信息量,而一个信源若由n个随机事件组成,n个随机事件的平均信息量就定义为熵(Entropy)。熵的准确定义是:信源X发出的xj(j=1,2,……n),
共n个随机事件的自信息统计平均(求数学期望),即H(X)=E{I(xj)} = =
H(X)在信息论中称为信源X的"熵" (Entropy) ,它的含义是信源X发出任意一个随机变量的平均信息量。
3.信息熵
信源X发出的xj(j=1,2,……n), 共n个随机事件的自信息统计平均(求数学期望),即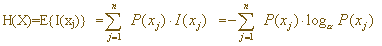
H(X)在信息论中称为信源X的"熵" (Entropy) ,它的含义是信源X发出任意一个随机变量的平均信息量。

更详细的说,一般在解释和理解信息熵时,有4种样式:当处于事件发生之前,H(X)是不确定性的度量;当处于事件发生之时,是一种惊奇性的度量;当处于事件发生之后,是获得信息的度量;还可以理解为是事件随机性的度量。
解释和理解信息熵有4种样式
(1) 当处于事件发生之前,H(X)是不确定性的度量;
(2) 当处于事件发生之时,是一种惊奇性的度量;
(3) 当处于事件发生之后,是获得信息的度量;
(4) 还可以理解为是事件随机性的度量.

下面为了巩固信息熵的概念,我们来做一道计算题。
例如:以信源X中有8个随机事件,即n=8。每一个随机事件的概率都相等,即P(x1)=P(x2)=P(x3)……P(x8)=  ,计算信源X的熵。
例如:以信源X中有8个随机事件,即n=8。每一个随机事件的概率都相等,
即P(x1)=P(x2)=P(x3)……P(x8)= 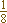 ,计算信源X的熵。 ,计算信源X的熵。

应用"熵"的定义可得其平均信息量为3比特
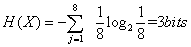
在明确了信息熵的含义后,我们下一个要思考的问题就是最需要解决的理论基础问题,统计编码的理论基础是什么?
香农信息论认为:信源所含有的平均信息量(熵),就是进行无失真编码的理论极限。信息中或多或少的含有自然冗余。
统计编码的理论基础是什么?

例如上例当P(x1)=1时,必然P(x2)=P(x3)=Px4)=P(x5)
=P(x6) =P(x7) =P(x8)=0,这时熵
H(X)=-P(x1)log2P(x1)=0
熵的范围
最大离散熵定理:所有概率分布P(Xj)所构成的熵,以等概率时为最大。
此最大值与熵之间的差值,就是信源X所含的冗余度(redundancy)。
可见:只要信源不是等概率分布,就存在着数据压缩的可能性。这就是统计编码的理论基础。
此最大值与熵之间的差值,就是信源X所含的冗余度(redundancy)。
可见:只要信源不是等概率分布,就存在着数据压缩的可能性。这就是统计编码的理论基础。
4.熵编码的概念

如果要求在编码过程中不丢失信息量,即要求保存信息熵,这种信息保持编码又叫做熵保存编码,或者叫熵编码。
特性:熵编码是无失真数据压缩,用这种编码结果经解码后可无失真地恢复出原图像。
如果要求在编码过程中不丢失信息量,即要求保存信息熵,这种信息保持编码又叫做熵保存编码,或者叫熵编码。
特性:熵编码是无失真数据压缩,用这种编码结果经解码后可无失真地恢复出原图像。
|