3.6.3.1 测量原理
Shaw对HRTF所做的测量工作最早起诸于1975年。Shaw选定了100位测试者, 其中大部分是男性, 分别来自五个不同的国家, 其年龄跨度超过40岁。Shaw给出了两种测量方法: 直接测量方法和间接测量方法。这两种方法各有其优缺点。下面对这两种方法作一简单的介绍。
(1) 直接测量方法
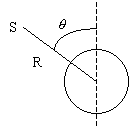
Shaw所测定的数据是从自由场到鼓膜的声压变化, 测试者坐在消音室里, 在测试者耳平面上有一个点声源, 如图3.47所示, 声源距测试者两耳联线中点的距离为R, 与垂直于两耳联线的纵轴所成方位角为θ, 声源发出频率为f的声波。在测试者左耳鼓膜处放置一个探针式微型麦克风用来测量左耳鼓膜处的声压值
。然后让测试者离开原位置,
在原测试者两耳联线中心处放置一麦克风测量自由场中的声压值
。那么从自由场到鼓膜的声压变化可以表示为:
那么与耳平面有关的声压变化值 可以用下式来表示:
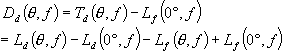
其中
、
、
、分别是在方位角为
时测量得到的参考值。Shaw还假定在一个实验中
不会发生很大的变化,
所以上述公式可以简化为: 
图3.47 声源与测试者的关系
(2) 间接方法
由于测量鼓膜处的声原值非常困难, 通常比较容易做到的是将探针式麦克风放在耳道的入口处或放在耳道中部, 将所测得的数据, 根据经验修正后来近似代替在鼓膜处测得的数据。这种方法最大的缺点是由于从耳道口到鼓膜处的传递函数无法精确测量得到, 因此这种方法会引起较为明显的误差。
3.6.3.2 用Shaw方法产生空间声
用Shaw方法产生空间声时, 首先必须给定声源在耳平面上相对于听者头部的方位角Q 和声源发出声音的频率f 。如果声源发出的是单一频率的声音, 那么其频率f很容易确定; 如果声源发出的是由多个频率的声音复合而成的声音, 那么就需要确定其基频。确定基频的算法是Ross提出的AMDF(平均幅度差函数)。AMDF算法一般是用于语音周期分析的。而对非语言声音信号，AMDF算法也能给出令人满意的结果。
当方位角和频率给定后, 从Shaw给出的表中可查到与耳平面有关的声压变化值
和方位角
为时的声压变化参考值
。如果给定的方位角Q
和频率f并不刚好是表中列出的值, 那么就只能查找最接近的近似值。然后计算在方位角为q，频率为f 时，从自由场到鼓膜的声压变化值
:
那么，如何利用从自由场到鼓膜的声压变化值
来计算三维真实感声音呢？在实际的应用中，我们的目标是要将一个单声道的声音文件转换成具有三维真实感声音的双声道声音文件。我们认为原始的单声道的声音文件是自由场中的声音,
生成出来的双声道声音文件则是到达鼓膜处的声音。前面已经提到, Shaw所提供的数据是对左耳测试得到的。因此直接利用Shaw数据可计算到达左耳鼓膜处的声音数据。根据头部的对称性,
方位角为q 是左耳的声压变化值应该等于方位角为了
时右耳的声压变化值, 相反方位角为q是右耳的声压变化值也应该等于方位角为了时左耳的声压变化值。至于到达右耳鼓膜处的声压变化值可以查找方位角为
时左耳的声压变化值得到。下面以计算左耳的声音数据为例, 设原始声音文件中的样本值为x , 计算后得到的到达左耳鼓膜处的声音文件的样本值为y。根据声学中的定义:
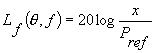
其中
是作为零声压级的参考声压值,
国际协议规定等于2×10-5
帕，根据公式
, 可得到: 
整理后得到:
此式给出了输入声音数据与输出声音数据之间的关系。我们可以根据这个数据关系来计算三维真实感声音。
用Shaw方法生成三维真实感声音文件具有计算量小的特点。但是Shaw方法所携带的数据量大, 而且只能计算给定的24个不同方位角和43种特定频率的声音, 具有很大的局限性。