在数字音频表示中，采用二进制编码是方便的，如表3.2所示。处于某一幅度范围内的模拟信号量化后被赋予某个确定数值。全部数据由一组二进制编码表示。表中的量化电平数为8，刚好用二进制的三位表示。二进制数的编码方法有多种。表1-10中采用的是二进制补码，它的最高位是符号位：0表示正,1表示负。
上述这种简单地把语音经模/数转换得到数字表示方法示意的是一种瞬时均匀量化器。它采用的编码方法称作脉冲编码调制(Pulse Code Modulation,简称PCM)。这是一种最常用最简单的编码方法。在MPC中就是用这种方法存储未压缩的音频数据。
在量化中，将量化值表示成
其中x(n)是未量化的样值，e(n)是量化误差(量化噪声)。那么量化噪声与哪些因素有关呢？对语音信号又有何影响？
首先我们假设语音抽样序列是离散时间随机过程的一个样本序列。这样我们就可以用统计观点来分析语音信号。
①用确定大量样值幅度直方图的方法估计语音信号幅度的分布密度。实测说明，它可以近似表示成拉普拉斯密度分布：
p(x)=
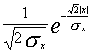
式中x代表语音信号，其均值为0，即
E[x(n)]=0
是语音信号的均方差。语音信号的方差σx2与自相关函数的关系是：2=E[x(n)-E[x(n)]]2=E[x2(n)]根据x与P(x)的关系, 可知语音样值的幅度分布密度随x的增大而减小。通过计算得出：信号幅度超过四倍均方差(4σx)的样值只有0.35%。信号幅度超过八倍均方差(8σx)的样值只有0.022%%。
②量化噪声的特点：语音信号是一个复杂信号，若量化阶距足够小，那么量化噪声与输入信号不相关，即
E[x(n)e(n+m)]=0 m为任意值
*量化噪声是平稳白噪声过程, 其均值为0, 且量化噪声之间不相关,即
E[e(n)e(n+m)]=σe2 m=0 σe是量误差e(n)的均方差
=0 其它
*对于阶距为△的均匀量化器, 量化噪声的幅度分布是均匀的, 量化误差与阶距的关系是:
=0 其它
③定义信号与量化噪声功率比的信噪比:
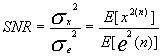
假设量化器量化范围是2xmax( x max为峰值)。量化器位数是B，则均为量化器的阶距△
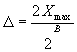
按上述噪声具有均匀幅度分布的假设，则：
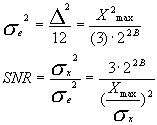
将信噪比用分贝表示：
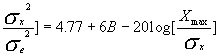
假设输入信号均方差σx的四倍则好是Xmax, 即Xmax=4σx，则上式变为：
SNR(dB)=6B-7.27
我们常用此公式近似计算量化器的信噪比，如：
B=6 SNR(dB)=28.85
B=8 SNR(dB)=40.89
量化器每增加一位编码，信噪比增大6dB。在高保真的音响系统中要求的信噪比大于90dB,那么模数转换至少需要16位。MPC中，常用的音频量化器位数是8和16。
在给定量化器码位的情况下，由于语音强度变化，清音与浊音幅度差异，实际所能达到的信噪比要小于计算值。如声音变轻，语音信号幅度减少到原设计值的1/2，即
，这时，语音信号幅度只有量化器设计范围的一半.虽然受限语音的抽样个数更少了，但对绝大多数抽样来说，量化后的最高位编码没有作用（似乎是B小了），致使信噪比下降。对于轻声段信号幅度大大下降，数字表示时只用了少数个码位，信噪比也大为减少。在实际应用中，我们希望有一个信噪比与信号电平无关的量化系统，那就要采用非均匀量化的方法。
脉冲编码调制(Pulse Code Modulation,简称PCM)，它是概念上最简单、理论上最完善的编码系统；是最早研制成功、使用最为广泛的编码系统；但也是数据量最大的编码系统。
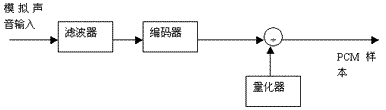
PCM的编码原理比较直观和简单，如下图所示。
在这个编码框图中，输入的是模拟声音信号，输出是PCM样本。其中的"滤波器"是一个低通滤波器，用来滤除声音频带以外的信号，"编码器" 是一个波形编码器，可以理解为一个采样器。
在3.1节中，我们知道，声音数字化的两个步骤是，采样和量化，采样就是每间隔一段时间就读一次声音信号的幅度，量化就是把采样得到的声音信号幅度转换为数字值。
量化可以分为两类：一类称为均匀量化，另一类称为非均匀量化。采用的量化方法不同，量化后的数据量也不同。因此，可以说量化也是一种压缩数据的方法。
采用相等的量化间隔对采样得到的信号做量化就是均匀量化。
对输入信号进行量化时，大的输入信号采用大的量化间隔，小的输入信号采用小的量化间隔，这样就可以在满足精度要求的情况下使用较少的位数来表示。声音数据还原时，采用相同的规则，这就是非均匀量化。
在非均匀量化中，采样输入信号幅度和量化输出数据之间定义了两种对应关系，一种称为m律压扩算法，另一种称为A律压扩算法。
下面的"瞬时压扩"内容介绍的就是非均匀量化器。
3.2.3.2 瞬时压扩
根据语音抽样非均匀分布的特点，设法让量化阶距随信号概率密度的减小而增大，或者说把大的量化误差留给出现概率小的样值，而得到较大的信噪比。一种非均匀量化器是瞬时对数压扩：量化前用对数函数将幅度压缩，解码后再用指数函数进行幅度扩张。其效果是量化器的信噪比对信号幅度不敏感。图3.2是对数编解码框图。
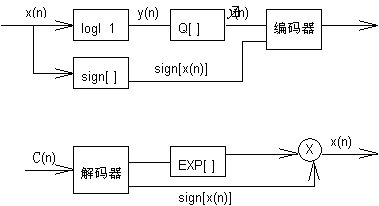
在编码器中，y(n)=ln|x(n)|
量化器的输出,
(n)=Q[ln|x(n)|]=ln|x(n)|+ey(n)
ey(n)是量化y(n)产生的误差,ln|x(n)|与ey(n)不相关。在解码器中，
(n)=ey(n)·sign[
(n)]=eln|x(n)|+ey(n)·sing[ (n)]
=|x(n)|·sign[x(n)]·eey(n)
=x(n)·eey(n)
当ey(n)很小时, 忽略eey(n)展开式的高阶次幂,上式近似表示为:
(n)=x(n)·(1+ey(n))=x(n)+ex(n)
量化器的信噪比:
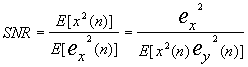
由于x2(n)与ey(n)不相关,所以
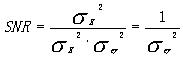
假如对y(n)采用均匀量化器, 那么:
即SNR只与量化阶距有关,而与信号方差无关, 分析可知,上述量化器需要元限多个量化电平, 是不能实现的。实用中采用修正的对数压缩，即μ律或A律量化器。
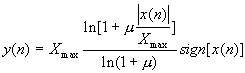
其中xmax是信号x(n)的是最大幅度,μ是控制压缩程序的参数。μ越大压缩越厉害。美电话中μ=225。可以推导出μ律量化器的信噪比：
SNR(dB)=6.02B+4.77-20lg[ln(1+μ)]-10lg[1+
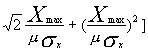
可以看出，μ律量化器的SNR能在较宽的
变化范围内基本不变。对非平稳的语音信号来说，相同码位的情况下，μ律量化器获得了较好的综合效果。还有一种类似的压缩规则--A律量化，
即：
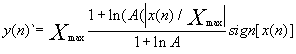
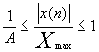
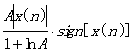
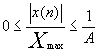
和μ律相比，A律压缩的动态范围略小些，在小信号时质量要较μ律差些。
μ律和A律量化是较为成熟的编码方法。早在1972年, CCITT以此原理为基础，推荐了话音编码标准G.711。它规定将13位或14位PCM编码转换成8位A律或μ律编码。还规定了μ律与A律的转换关系。这个标准已应泛用于数字电话系统中，以及可视电话、电视会议系统中。
μ律（m-Law）压扩主要用在北美和日本等地区的数字电话通信中。m为确定压缩量的参数，它反映最大量化间隔和最小量化间隔之比，通常取100≤m≤500。由于m律压扩的输入和输出关系是对数关系，所以这种编码又称为对数PCM。
A律（A-Law）压扩主要用在欧洲和中国大陆等地区的数字电话通信中。A为确定压缩量的参数，它反映最大量化间隔和最小量化间隔之比。A律压扩的前一部分是线性的，其余部分与μ律压扩相同。