在通讯和信号处理技术中有一个经常遇到的问题是：怎样从受到噪声及各种干挠沾污的信号中的不需要成分予以抑制，而把所需要的有用信号分离出来。其中的一个方法是利用有用信号和需要抑制的成分之间在频谱上的差别，设计一个系统使接收到的信号通过该系统后，有用信号的成分保持不变而其它成分则大于衰减，这样的系统称为滤波器。

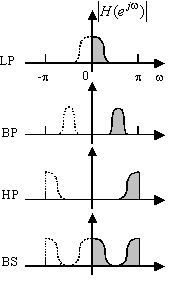
　　滤波器的类型：滤波器按其频率特性可区分为：低通、高通、带通与带阻四种类型。理想滤波器的频率特性 |H(jw)|，其通带与阻带之间的界线应该是截然分开的，也就是说其特性应该有很陡的斜率。图6.7就是四种类型滤波器的理想幅频特性（或幅度特征）示意图。其（a）为低通，（b）为高通，（C）为带通，（D）为带阻。

　　以低通滤波器为例，它的理想幅频特性是一个矩形。这就是说频率低于 的信号成分，可以全部衰减到零，而频率低于 的信号成分，全部都在输出端复现。具有这样理想特性的低能滤波器在物理上是不可实现的。人们无法用实际的电子元器件来组成这样理想特性的实际系统。为此，只能设计出尽可能逼迫理想的幅频特性同时又能满足因果律的实际系统。实际滤波器的幅频特性允许如图下图所示。

　　为了使其特性尽可能接近理想特性，对实际滤波器的指标要求为：通带内的幅度起伏要小，阻带内的衰减要大，过渡带应尽可能地窄。寻找一个系统函数，使其幅度特性能接近于所要求的理想特性，属于滤波器设计中的逼近问题，这方面已做了大量工作，并且已有不少性能良好又便于使用的滤波器研究出来，并造成具体的表格，可以根据对滤波器特性的要求，从技术经济的合理性来设计选择。