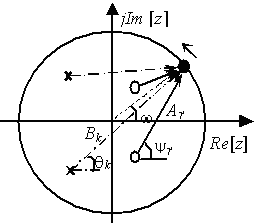
图6-9 系统频率响应的几何确定法
如图6-9所示,显然如果单位圆上某个点沿逆时针方向不断转动,转动一周就可以根据式得到系统的频响。另外,由于位于原点的零点或极点到单位圆上任一点的距离都是1,因此,在z平面原点外加入或去掉零、极点,将不会影响系统的幅频特性,而只会影响系统的相频特性。
![]() 例:考虑在单位圆内有一对共轭极点
例:考虑在单位圆内有一对共轭极点
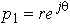 和
和 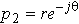 (其中
(其中 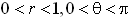 )的离散LTI因果稳定系统,其传递函数为
)的离散LTI因果稳定系统,其传递函数为
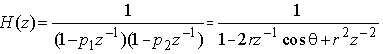
求其频率响应,并以 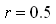 和
和 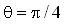 为例用几何作图法大致确定其幅频响应曲线的形状。
为例用几何作图法大致确定其幅频响应曲线的形状。
解:由于传递函数的ROC包括单位圆,因此系统的频响可直接求得为
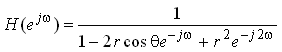
当 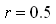 和
和 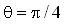 时,系统的传递函数有一个二阶零点0(用几何作图法求幅频特性时可以不考虑)和一对共轭对称的极点
时,系统的传递函数有一个二阶零点0(用几何作图法求幅频特性时可以不考虑)和一对共轭对称的极点
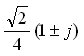 。于是可以求得系统的幅频响应如图6-10右所示。
。于是可以求得系统的幅频响应如图6-10右所示。
图6-10 二阶系统的幅频响应(
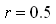 和
和
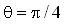 )
)
在上图中,我们发现在 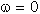 处有一个“谷”,而在
处有一个“谷”,而在 ![]() 中间有个“峰”。如果再多画几幅图,我们会发现,
中间有个“峰”。如果再多画几幅图,我们会发现,
![]() 越小(即极点越靠近原点),那么谷与峰之间的过渡越陡峭;反之越平坦。这就是说,设定不同的
越小(即极点越靠近原点),那么谷与峰之间的过渡越陡峭;反之越平坦。这就是说,设定不同的
![]() 值,系统既可作为一个低通系统,又可作为一个带通系统。
值,系统既可作为一个低通系统,又可作为一个带通系统。