例：已知一个因果的离散时间系统的差分方程为

　　试（1）求系统的传递函数 以及相应的收敛域；
　　　（2）根据传递函数说明系统是否是稳定的；
　　　（3）求解系统的单位冲激响应。

　　解：（1）求传递函数及其收敛域。

　　为了求系统的传递函数，先对系统差分方程两边取Z变换：

　　这样，根据系统传递函数 的定义，可得

　　容易看出，函数H(z)有两个一阶零点 、 和两个一阶极点 。由于要求H(z)对应的单位冲激响应序列是因果的，H(z)的收敛域至少应是 ；又由于 时， 是有限值，所以 的收敛域可以无穷远点 ；因此最终的收敛域为 。

　　（2）判断系统的稳定性。考虑传递函数的ROC，单位圆内在其中，根据我们前面已经证明的结论，这样的系统是稳定的。

　　（3）利用部分分式分解法，可以将H(z)分解为下面的部分分式的形式

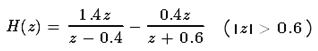
　　对各子式分别求逆Z变换，可得相应的时域序列，也即传递函数对应的单位冲激响应（序列）

　　（2）根据传递函数零极点分布求系统频率响应特性

　　（a）频率响应的概念:

　　所谓系统的频率响应，简单的说，就是系统对输入信号的频谱的影响（改变）特性。前面我们已经知道，对线性时不变系统，输出信号是输入信号与系统单位冲激响应的卷积；而根据第二章关于傅里叶变换性质中的卷积定理，时域卷积，频域乘积 。这种频域乘积相当于对信号的频谱进行加窗，对不同的频率分量，窗函数乘不同的系数。这样就可以把一些不关心的频率成分过滤掉。因此，系统的频率响应，实际上指的就是系统单位冲激响应的傅里叶变换频谱。

　　（b）幅频响应特性分类

　　按照系统的幅频响应特性（即系统单位冲激响应的傅里叶变换），可以将系统分为低通滤波器、带通滤波器、高通滤波器、带阻滤波器、全通滤波器。

　　对连续时间系统而言，按不同的幅频响应特性，相应的示意图如下：

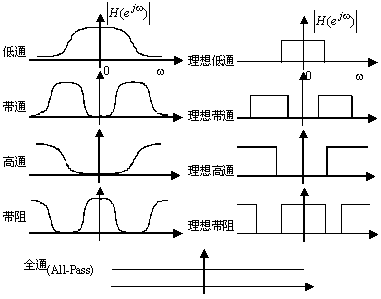
图6-7 连续时间系统按幅频响应分类(示意图)